Electrical Discharges

How the spark, glow and arc work

Contents

1. Introduction: fundamental processes
2. The Voltage-Current Characteristics
3. The Spark: Breakdown: electron avalanche, Townsend discharge, Paschen's Law, Geiger-Müller tube
4. The Glow Discharge: cathode phenomena, positive column, laser pumping, similitude, sputtering
5. The Arc Discharge: cathode phenomena, low- and high-pressure plasma, negative resistance, carbon arc in air
6. Applications of Arcs: welding, lamps, rectifiers, switching, protection, fuses.
7. References

An electrical discharge results from the creation of a conducting path between two points of different electrical potential in the medium in which the points are immersed. If the supply of electrical charge is continuous, the discharge is permanent, but otherwise it is temporary, and serves to equalize the potentials. Usually, the medium is a gas, often the atmosphere, and the potential difference is a large one, from a few hundred volts to millions of volts. If the two points are separated by a vacuum, there can be no discharge. The transfer of matter between the two points is necessary, since only matter can carry electric charge. This matter is usually electrons, each carrying a charge of 4.803 x 10^-10 esu. Electrons are very light, 9.109 x 10^-28 g, and so can be moved with little effort. However, ions can also carry charge, although they are more than 1836 times heavier, and sometimes are important carriers. Where both electrons and ions are available, however, the electrons carry the majority of the current. Ions can be positively or negatively charged, usually positively, and carry small multiples of the electronic charge.

Electrical discharges have been studied since the middle of the 19th century, when vacuum pumps and sources of current electricity became available. These laboratory discharges in partially-evacuated tubes are very familiar, but there are also electrical discharges in nature, lightning being the primary example. There are also the aurora borealis and australis, St. Elmo's Fire, sparks from walking on a rug in dry weather and rubbing cats, crackling sounds when clothes fresh from the dryer are separated, and similar phenomena, many resulting from the high potentials of static electricity. Technology offers a wealth of examples, such as arc welding, the corona discharge on high-tension lines, fluorescent lamps, including their automatic starters, neon advertising signs, neon and argon glow lamps, mercury and sodium lamps, mercury-arc lamps for illumination and UV, carbon arc lights, vacuum tubes, including gas-filled rectifiers, Nixie numerical indicators and similar devices. Some of these are historical, but all are interesting and often fascinating to watch.

A good reason for this article is also that information on electrical discharges is not easy to find in current literature, in spite of their importance in many fields of physics, astrophysics, atmospheric electricity and engineering. The McGraw-Hill Encyclopedia of Physics has no entry for "electrical discharge" or "electric arc," for example. The closest one can come are articles on plasma physics, which do not do the job. Plasma physics, as it is generally presented, is a rather limited field mainly concerned with the luckless search for thermonuclear power. Every day we see many examples of discharges--street lights, neon signs, fluorescent lamps--so how they work must be valuable knowledge.

The two termini of a discharge are at different potentials. The higher, or positive, potential is at the anode, while the lower, or negative, potential is at the cathode. These electrodes are often conductors, but need not be. In a thunderstorm, a cloud electrode may simply be a region of excess charge distributed over a volume. These names were given by Michael Faraday, with the help of the classical scholar William Whewell, when he began to study electrochemistry and electrical discharges in the 1830's. The word "anode" is from the Greek "aná-hodos" or "way in," while "cathode" is from "katá-hodos," or "way out." Electrode is a later creation for "electro-hodos" or "electric way," and is noncommttal as to the positive direction of the current. The conventional current is in the direction of positive charge, so electrons actually leave at the "way in" and enter at the "way out."

Unless otherwise stated, we shall assume that the medium is a gas predominantly composed of neutral molecules (we won't distinguish between molecules and atoms), which we usually treat as ideal. Then, the pressure p of the gas is simply related to its number density n by p = nkT, where T is the absolute temperature, and k is Boltzmann's Constant, 1.38 x 10^-16 erg/K. If T is in K, and n is in cm^-3, then p is in dyne/cm². In technical work, gas pressure is measured in mmHg, and 760 mmHg is atmospheric pressure, 1.0123 x 10⁶ dyne/cm³, from which the conversion can be derived. At one atmosphere and 273K, the number density in a gas is 3.22 x 10¹⁸ cm^-3, which is the same for all gases (Avogadro's Law). The gas is normally electrically neutral, and contains neither ions nor electrons, and so is a nonconductor. In daily life, we rely on the air to be an insulator in our dealings with electricity.

The electrons, ions and neutral molecules are in incessant thermal motion, because their collisions are perfectly elastic. In equilibrium, the velocities are distributed according to the Maxwell distribution, f(v) = (m/2πkT)^3/2exp(-mv²/2kT)4πv², which integrates to unity with respect to dv. The electron temperature T_e is usually very different from the ion and neutral temperature T_n at low pressures, because the electrons receive more energy from the electric fields in a discharge, and can exchange kinetic energy with the neutrals only with great difficulty, so they represent a reservoir of kinetic energy that is in very weak contact with the neutrals. The much greater mass of the ions and neutrals also means that they move at much lower velocities. Speeds given to the electrons by electric fields are often very much greater than thermal speeds, especially near the cathode, where the electric field is very high. These electrons, naturally, do not have a Maxwellian distribution until they have lost most of their energy in inelastic collisions and ionization. The rms velocity √(3kT/m) is the velocity of a particle with the average energy. Approximately 60% of the particles have less energy, 40% more. The average kinetic energy of a particle at temperature T is (3/2)kT.

If V is the difference in potential between the anode and cathode, and d is the distance between them, then the average potential gradient, or electric field, is V/d. Again, in technical work, V is measured in practical volts, the familiar ones in which a flashlight battery supplies 1.5 V. The Gaussian unit is the esu, about 300 V, which appears in theoretical arguments. Therefore, the field E will be in V/cm, or in statvolt/cm, and the conversion between them is easy. This average field will drive a positive ion in its direction, an electron in the opposite direction.

For a discharge to occur, there must usually be a source of electrons at the cathode, and the nature of this source controls the form of the discharge. Cosmic rays and natural radioactivity continually produce a small number of electrons and ions in all gases at the surface of the earth, and this gives air a small conductivity. The electrons will migrate to the anode, the ions to the cathode, and a small current will flow. This current has no visible effects, and can be detected and measured only with difficulty, but is always present. Any charged body attracts charges of the opposite sign that sooner or later will neutralize its charge, though the usual reason for the loss of charge is conduction over the surface of the supports of the body, which is normally far greater than the small space current from the ions and electrons normally present in the air.

More copious sources of electrons are necessary for a good discharge. One source is the photoelectric effect, when light of sufficiently short wavelength falls on a metal or semiconductor and liberates a photoelectron. Photons can also be absorbed by a molecule, which gives up an electron and becomes a positive ion. The photon energy hν must be greater than the energy required to free the electron, the work function. Thermionic emission, the emission of electrons by a heated body, can supply heavy currents. The body must be heated to incandescence, and for efficient emission, its work function must be low. Tungsten has a work function of 4 eV, and has long been used as an electron emitter, since it also has a high melting point. Alkali metals have a small work function, but cannot be used by themselves because of their low melting points. Electrons striking a metal surface can knock loose secondary electrons readily, but this is of little use for discharges, since the electrons impact the anode, and secondary electrons would simply fall back into the anode, not add to the discharge current. However, positive ions can also create secondary electrons. Although this is not an efficient process, it produces electrons at the right place and can support a discharge.

Electrons already in the discharge, such as the random electrons produced by cosmic rays and radioactivity, can add to their number by ionizing gas molecules by collision. Each ionizing collision produces a new electron, and a positive ion that moves the other way, an ion pair. An electron cannot do this unless it has acquired sufficient kinetic energy by being accelerated in an electric field. There are two ways this can be done. If the electron makes no collisions, even a small electric field will allow it to accumulate energy in a long-enough run. In this case, KE = mv²/2 = eEx, where E is the field and x is the distance travelled. Electron energies are often quoted in electron-volts, abbreviated eV, and such that the energy U in eV is given by eU = eEx, so that U is just the potential drop in the distance x. On the other hand, if the probability of collision of the electron in a distance dx is dx/L_e, where L_e is called the electron mean free path, and L_e is much smaller than the distance x, then the speed of the electron is given by v = KE, where K is the electron mobility, in cm/s per V/cm, for example. Then, the only way for the electron to accelerate is to find a larger field E.

The mean free path L is inversely proportional to the pressure, so pressure has a great effect on how an electron gains energy. The molecules of the gas also have a mean free path, but since molecules are larger, their mean free path L is shorter than L_e. As an estimate, we can take L_e = 5.64L. In Ne, the mean free path at 760 mmHg and 273K is 1.93 x 10^-5 cm, while in air it is 9.6 x 10^-6 cm. By "air" we mean the usual mixture of nitrogen and oxygen, and the values are an average.

The energy required to ionize neon, called the ionization energy, in the reaction Ne → Ne⁺ + e^-, is 21.559 eV, and to knock two electrons off requires 41.07 eV. To raise a Ne atom to its first excited state requires 16.58 eV, which is called the resonance energy. This gives an idea of the energy required to produce an ion pair. Since most collisions do not result in ionization, and there are many ways to fritter energy away uselessly, the average energy per ion pair produced is greater than the ionization potential, rather closer to twice this value. To give an electron sufficient energy to ionize Ne at one atmosphere, the field strength would have to be E = 21.559/(5.64)(1.93 x 10^-5), or about 200,000 V/cm, an extremely high field that would have some untoward effects. At 1 mmHg, the field would have to be 260 V/cm, a more tractable value.

The energy required to excite a molecule or atom to its first excited state above the ground state is called the resonance energy, and is, of course, less than the ionization energy. The inert gases, which have a closed shell of electrons in the ground state, have very large resonance energies. For He, it is 19.81V, and for Ne, 16.62 eV. These levels are also metastable, which means that a transition to the ground state by radiation is difficult, and they may retain their excitation energy for an extended period, perhaps until they collide with a wall, or experience another collision with an electron or atom. This makes cumulative ionization possible, where an atom can be ionized by multiple collisions in which the electrons have insufficient energy to ionize in a single collision. The energy of a metastable can be transferred to a different atom or molecule by a collision of the second kind. Alkali metals, with a single s electron outside a closed shell, have very low resonance potentials. For sodium, V_i = 5.138V and V_r = 2.102V. For caesium, the figures are 3.893V and 1.39V, respectively. Mercury, often used in discharges, has V_i = 10.43V and V_r = 4.67V, and the lowest excited states, ³P's are metastable to the ¹S ground state (but still give a strong ultraviolet line). The spectroscopic notation is included for those who will appreciate it. The fundamentals of atomic structure and spectra are important in understanding discharges.

The emission of light is one of the principal characteristics of discharges. Light of a definite frequency is emitted when an excited atom falls to a lower energy level. If there is an electric dipole transition moment, then the transition is called allowed, and occurs in about 10^-8 s if nothing intervenes. The collision frequency is about 10¹¹ per second at atmospheric pressure, so usually the excitation energy is lost in a collision before it can be radiated. At 1 mmHg, however, the collision frequency is comparable to the radiation lifetime, and radiation is a possibility. Radiation is always a competetion between de-excitation processes. If the dipole transition moment is forced to be zero by symmetry considerations, then radiation may occur by other means, such as magnetic dipole or quadrupole radiation, but the radiative lifetime for these is much longer, so they are not seen even at 1 mmHg pressure. These are forbidden transitions. They are not really forbidden, just improbable. At higher pressures, excited atoms are continually affected by collisions, which broaden the lines emitted. At still higher pressures, the atom states are smeared out, and the radiation begins to assume the characteristics of black-body thermal radiation.

Mercury has strong lines at 253.65 nm, 404.66 nm, 407.78 nm, 435.84 nm, 546.1 nm, 576.96 nm and 579.06 nm (and many others not as strong). The first is the resonance line in the ultraviolet that strongly excites fluorescence, and the next two are at the short-wavelength limit of human vision. The cyan line at 436 nm, the green line at 546 nm, and the yellow doublet at 577 and 579 nm can easily be seen in the spectrum of a fluorescent tube, and should be familiar to all. They can be separated by filters for use in optics experiments, and this was commonly done before the He-Ne laser appeared around 1971. The 254 nm, 408 nm and 577 nm lines are all "forbidden" by the usual selection rules, but happen to be very strong in Hg, where singlet-triplet combinations among lower levels are not very forbidden.

If an electron frees another by an ionizing collision, then these two can both free additional electrons, and so on. This creates an electron avalanche, which may send a burst of electrons toward the anode, leaving in their wake a cloud of slow positive ions that will make their way to the cathode. The net result is to multiply the original electron current, an effect used in gas phototubes to increase the photocurrent for a given amount of light. This does not start a sustained discharge, but merely increases the current that otherwise would be available. This type of discharge produces little light, so it is called a dark or Townsend discharge, after the man who studied them in detail first.

That cloud of positive ions will sooner or later collide with the cathode. It is rather unlikely for a positive ion to snatch an electron from the few that are available while it is moving through the gas. Recombination is a very difficult process, since only one particle is the outcome, rather than the three particles that come out of an ionization, so it is hard to conserve both momentum and energy. Therefore, most of the positive ions created in an electron avalanche reach a surface eventually, and they are driven to the cathode by the electric field. When they arrive, they recombine at the surface, and in some cases eject an electron. For Ne on an Fe cathode, one out of about every 45 ions produces an electron. However, if the electron avalanche produces more than 45 electrons, then there will be sufficient positive ions to replace the electron that originally left the cathode (or came in from elsewhere). Now the discharge produces its own electrons, without relying on cosmic rays or natural radioactivity, and becomes self-maintained. This is a significant event in the life of a discharge, and usually means that the discharge becomes evident through light or noise. The potential between anode and cathode at which this occurs is called the sparking potential V_s. Now the whole path between anode and cathode becomes conducting because of the electrons and ions distributed along it.

Unless something limits the current, such as the disappearance of the potential difference, it increases rapidly and without bounds. The ion bombardment heats up the cathode surface, which becomes incandescent, and begins to emit electrons thermionically, without reference to the number of ions coming in or the efficiency of the electron avalanche. Any spot that becomes hotter than its neighbor, tends to become even hotter as the extra thermionic electrons attract the positive ions to the spot. This, the final state of the discharge, is called an arc. The name came from the way the path of the discharge, when arranged to be horizontal, rose in a flaming arch, or arc. It requires very little potential difference to support the arc, mainly just enough to keep the path of the discharge supplied with ions to replace those lost in various ways. A lightning stroke is an example of such a discharge, but with anode and cathode that are quite different from those in a carbon arc light. In the carbon arc light, the discharge is started by drawing the carbons apart, which produces an arc at once, since the discharge does not have the difficult task of establishing a conducting path over a great distance, as in lightning. An arc is also produced whenever an electric circuit is interrupted, and must be extinguished before it does any damage.

The nature of a discharge depends, as we have seen, on the method for supplying electrons at the cathode, and on how the discharge is confined. The lightning stroke, and the carbon arc, are both unconfined arcs. The lightning stroke draws its electrons from the cloud, its cathode, and transmits them to the earth, its anode. The carbon arc obtains its electrons from the cathode spot on the negative carbon, which it heats to incandescence. Both are self-confined, the surface of the conducting channel arranging itself so that the net outward current is zero. A discharge between metal electrodes in a glass tube that gets its electrons from positive-ion bombardment of the cathode, and is confined by the glass walls, is called a glow discharge. Glow discharges are useful and convenient to study, so their properties are very familiar, if not those of the majority of discharges. A discharge may exist in the vicinity of a sharp point, or other place with a small radius of curvature where the electric field is increased significantly from its average value. A negative potential on the point makes it a cathode, while the anode is an indefinite volume in the surrounding gas. A positive potential makes it an anode, and attracts electrons from an indefinite surrounding volume, which becomes the cathode. These two discharges look quite different with constant potentials, but with alternating current the opposites succeed one another and make an average impression. If the discharge occurs at about atmospheric pressure, it is called corona.

In any discharge, multiple processes compete at the electrodes and in the gas, so explanations and theories can become subjects of dispute. A theory usually takes into account only the principal process operating under the conditions of the problem, and this is often quite satisfactory. Sometimes different assumptions and mechanisms can lead to the same outcome, which further complicates things. The reader should keep in mind that complete explanations are probably impossible in many cases, and we must be satisfied with qualitative or semi-quantitative results. Also, the variety of phenomena in discharges is very rich and depends on many factors, such as purity and surface preparation, that are difficult to quantify. The whole variety cannot be mentioned here, only what is typical under reasonable assumptions. There is great scope for thought and reasoning in this field, which makes it fascinating, along with the beauty of the phenomena.

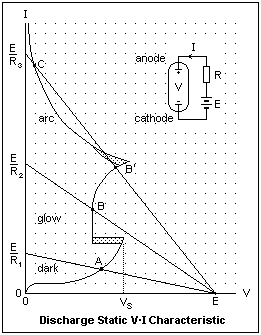Let's now consider a typical laboratory discharge, taking place in a glass tube with metallic electrodes. The nature of the electrodes has little effect on the characteristics of the discharge. Commonly-used materials are carbon, platinum, iron, nickel or tungsten. The voltage source E is connected in series with a current-limiting resistance R, so that the voltage between anode and cathode is V = E - IR. This relation is expressed by the load lines in the diagram, for values of R equal to R₁ > R₂ > R₃. The irregular curve is the V-I characteristic of this device, distorted to show the various regions conveniently. Point A is a stable point of operation for R = R₁. This can be seen as follows: suppose the current I to be slightly reduced for some reason. Then V becomes greater, according to the load line, while the voltage between anode and cathode becomes smaller. The difference in voltage acts to increase the current, restoring it to the value before the disturbance. If the current is slightly increased, we find a voltage deficit, which reduces the current, again bringing the operating point back to the original place. This will always happen if the V-I curve is more steeply inclined than the load line. At point A, the current is no more than a microampere, the discharge is dark, and is not self-sustained. We are in the Townsend region.

Now imagine R reduced steadily from R₁ to R₂. Point A moves up the curve until the sparking potential is reached. Now the voltage is sharply reduced, and the operating point is B, which is stable. The discharge is now self-sustaining as a glow discharge, and cathode heating is not sufficient to cause transition to an arc. If R is further decreased, towards R₃, the voltage across the discharge increases until point B' is reached. Although B' is stable with respect to small fluctuations, cathode heating may be enough to increase the electron supply and lower the discharge voltage. This change is cooperative, and the discharge quickly moves to point C, where V is lower and I is greater. This is the arc, and operating point C is stable. However, if R is further reduced, the current will increase without bound until something melts. The regions where the discharge type changes are shown cross-hatched, to show that the actual values may not be clearly defined. This characteristic tells a lot about the circuit behavior of discharges, but it does not say much about the dynamic relations, only about the stable operating points. We shall discuss each of the principal discharge species below.

Let's begin by analyzing the initial breakdown of the discharge, that produces the spark. We assume that every electron emitted from the cathode creates an avalanche, and that the positive ions from this avalanche return to the cathode and liberate new electrons to join the discharge. Suppose n_o electrons start at the cathode, and at a distance x they have multiplied to n. The electrons added to the avalanche in a distance dx will be dn = αndx, proportional both to the number of electrons, and to the distance dx. The factor α is the probability of creating a new electron per unit length (or, the average number of electrons created per cm of path), and is called the first Townsend coefficient. If α is constant, we can integrate the relation to find that ln n = αx + C, and determine that C = ln n_o, so that ln (n/n_o) = αx or n = n_oe^αx, the equation for exponential growth.

The number of electrons that arrive at the anode will be n = n_oe^αd, where d is the distance from the cathode to the anode. In general, α will be a function of the electric field E, but here we assume E is constant, so our equation holds exactly only for plane-parallel electrodes and in the absence of space-charge effects. Nevertheless, it will give us order-of-magnitude results. The number of positive ions produced in the avalanche will be n - n_o. We assume that all return to the cathode, where they release γ(n - n_o) new electrons. The factor γ expresses the efficiency of the ions in liberating electrons. This means that the net number of electrons leaving the cathode will be n_o + γ(n - n_o), and the number eventually reaching the anode will be n = [n_o + γ(n - n_o)]e^αd. If we solve for n, we find that n = n_oe^αd/[1 - γ(e^αd - 1]. If e^αd is much greater than 1, we have simply n = n_oe^αd/(1 - γe^αd).

If e^αd increases to 1/γ, the denominator vanishes, and the number of electrons reaching the anode increases without limit. This is the sparking or breakdown point. The dependence of α on the electric field E is described by the empirical formula α/p = Ae^-Bp/E, where A and B are constants, p is the pressure, and E the electric field. The pressure comes in because the important thing is the energy gained in a mean free path, EL, and L is inversely proportional to pressure. Therefore, if the pressure changes, Bp/E will remain constant. α itself depends on collisions, and will be proportional to the pressure for the same reason. Therefore, α/p will be constant, as will Ap, as the pressure changes. Hence, the constants A and B need be determined for only one pressure. The dimensions of A are mmHg^-1 and V/cm-mmHg, respectively. For air, A = 14.6 and B = 365, and for helium A = 2.8 and B = 34. These figures hold only over certain ranges of electric field, of course. The factor γ for air on a nickel cathode is 0.036, for neon 0.023, which are typical figures.

We can now estimate the sparking potential by finding the value of E for which e^αd = 1/γ. The condition is ln(1/γ) = αd = Apde-Bpd/V_s, which we solve for V_s. This gives V_s = Bpd/ln[Apd/ln(1/γ)], or C¹(pd)/ln[C²(pd)] in terms of new constants that can be tabulated. The striking thing about this relation is that the sparking potential is a function of the product pd only. This is called Paschen's Law. Moreover, by setting the derivative of V_s with respect to pd equal to zero, we find that the sparking potential has a minimum when C₂pd = 1, or pd = e ln(1/γ)/A.

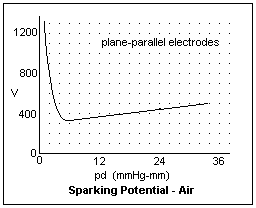The sparking voltage as a function of pd for air is shown in the graph at the right, showing a minimum at 327 V at pd = 5.67 mmHg-mm. From the ionization constants for air, we find 266 V using the above equation, which is not bad agreement. At pd = 2000 mmHg-mm the sparking voltage is 10kV, and at 4500 mmHg-mm it is 20kV. The figures are for plane-parallel electrodes, so they give the sparking voltages for the corresponding values of field strength.

We have assumed the mechanism of breakdown to be electron avalanches and positive-ion production of electrons at the cathode. The excited positive ions could also emit radiation that would eject photoelectrons from the cathode with the same effect. Therefore, the fact that we have cooperative amplification of the electron current does not unambiguously determine the mechanism. This occurs often in the study of electrical discharges, and often mechanisms are obscure while their effects are well-known.

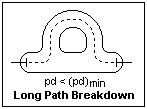The minimum of the sparking potential has a strange consequence. For values of pd to the left of the minimum, if the discharge has a choice of two paths of different lengths, it will choose the longer path because it breaks down at a lower voltage (to the right of the minimum), as shown in the figure. In this case, bringing the electrodes closer together can actually increase the breakdown voltage.

At low pressures, breakdown occurs with a silent spark of fine filamentary form. At high pressures, the spark is bright and noisy. Breakdown can occur as the voltage is raised, or the cathode-anode distance is increased or the pressure reduced (for pd to the right of the minimum). Space charges can cause the voltage distribution to change, and increased fields have the same effect as an increase in the overall voltage. Lightning shows progressive breakdown over a long path by this mechanism. A simple increase in primary ionization that raises n_o will not cause breakdown by itself. Sparks have chemical effects, creating ozone and nitrogen oxides in air because of the ionization and excitation, and initiating chemical reactions.

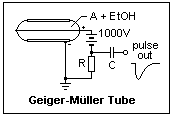The Geiger-Müller counter tube is an interesting example of breakdown characteristics. It consists of a cylindrical metal cathode with a fine wire anode on the axis, as shown in the diagram. The thin window for entry of β particles (electrons) is not shown, if the counter is designed for this purpose. The counter also detects γ rays, that eject photoelectrons from the cathode, undergo Compton scattering, or create electron-positron pairs. The GM counter is not a sophisticated instrument, but has the great advantage of giving a large pulse that can even be heard directly through earphones without amplification. It is filled with Argon and a little ethyl alcohol vapor.

The creation of a free electron in the volume of the counter or at the cathode initiates an avalanche discharge that generally involves the whole length of the tube. The electrons are collected by the anode wire causing the leading edge of the pulse, and then the ions move more slowly to the cathode, making the pulse tail. The ions are swept out in about 100 μs, during which the tube is insensitive. The maximum counting rate is about 5000 counts/s, and the loss of counts because of the dead time is called the coincidence loss.

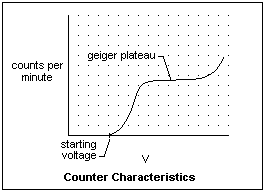If the counting rate with a certain source is measured as a function of the voltage applied to the tube, a characteristic like the one in the figure is found. Counting begins at the starting potential, when the electric field is first strong enough to support an avalanche. The counting rate increases until the Geiger threshold, and remains nearly constant across the Geiger plateau. It is the existence of this plateau that allows the instrument to be calibrated. All the discharges in this region are of similar strength. If the ions liberated a sufficient number of electrons at the cathode, the discharge would become self-sustaining, rendering the tube inoperative. To prevent this, a quenching gas, often ethyl alcohol, but also a halogen such a chlorine or bromine, that sucks up electrons is added. The GM counter is between a Townsend discharge on one hand in which the current depends on the ionization, and breakdown, where the discharge is self-maintained. At a sufficiently high applied voltage, however, a glow discharge cannot be avoided.

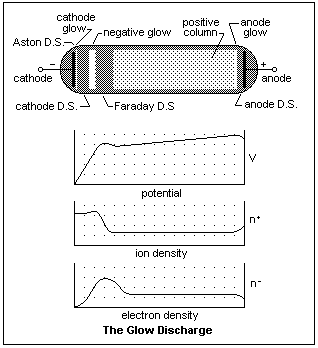If we reduce the gas pressure to between 1 mmHg and 1 cmHg, we get a glow discharge that looks like the one in the diagram, a typical low-pressure glow discharge. If we started with the pressure at atmospheric, we would find it impossible to start a discharge with, say E = 300 V. As we pumped the tube down, at some point a discharge would start, filling the tube with pink light, if the gas was air, but the current would be low and the light not intense. With further evacuation, the current would increase as the voltage across the tube decreased, and we would see a dark region coming out of the cathode. Continuing, the dark region would increase in width, and the cathode would seem to be covered with a soft bluish light. The light of the pink column may begin to fluctuate in moving waves. At the pressure mentioned above, the voltage across the tube would be least and the current greatest, and this is the discharge state shown in the diagram.

At lower pressures, the dark region would expand proportionally to the reciprocal of the pressure, the glow around the cathode would also expand, and perhaps a dark region between it and the cathode would become evident. The pink column of light would grow steadily shorter, and eventually be swallowed up by the dark zone. Now the glass of the tube might begin to fluoresce green where fast electrons struck, and the voltage across the discharge would rise as the current fell. The electron mean free path is now comparable to the dimensions of the tube. Finally, the glow at the cathode would flicker and go out, and the discharge would cease, as the electrons could find no molecules to ionize as they traversed the tube from end to end.

The names of the various regions are shown on the diagram. There are two principal parts of the discharge. At the left, the region between the cathode and the Faraday dark space (D.S.) is the engine that drives the discharge, creating the necessary electrons. If we lengthen the tube, this region does not alter, but remains the same. At the right, the region between the Faraday dark space and the anode serves to connect the electron engine with the anode with a conducting path. It is almost electrically neutral, a plasma confined between the walls, the anode, and the Faraday dark space. It is surrounded on all sides by what is essentially a plasma sheath that cuts off current to the walls (which assume a negative potential relative to the plasma), allows just the right amount of electron current to go to the anode, and to come from the Faraday dark space.

The cathode is bombarded by positive ions coming mainly from the negative glow region, where they are created by collisions with fast electrons. These ions recombine at the cathode, then fall to the ground state with the emission of light. This light constitutes the cathode glow, which is separated from the cathode by a very narrow dark interval, the Aston dark space. The "dark" regions are not really dark, just less luminous than the bright regions. The cathode dark space has the strongest electric field in the discharge, which increases proportionally to the distance from the cathode. This region is filled with a positive space charge of ions moving in the other direction. When the electrons acquire sufficient energy to ionize, they begin to do so as they enter the negative glow, the brightest part of the discharge. In the width of the negative glow, all the positive ions that the discharge needs are continually being created, and then they are accelerated towards the cathode. Even the ions may be excited by the fast electrons, and both the neutral and ionized molecules contribute to the light. The electrons are exhausted by this effort, and drift out into the Faraday dark space at low velocity. There are now much fewer ions around, so the electrons can be accelerated in the gentle field. As they speed up, their number density goes down. Except close to the cathode, the electrons carry practically all of the discharge current. When they have sufficient energy to excite the molecules of the gas, the emitted light becomes evident. This light is produced with minimal excitation, and consists only of light emitted by neutral atoms which have been excited above their resonance energy, which explains its different character from the light emitted by the negative glow.

From here to the vicinity of the anode, the potential gradient must only be sufficient to allow the most energetic electrons to form ions to replace those that diffuse to the walls. The electrons carry most of the discharge current in this region, the ions mainly just ensuring electrical neutrality. As the anode is approached, adjustments must be made to suit the anode current. The random electron current may be larger than required, so the electrons must be slowed down by an extra electron density near the anode, or, alternatively, a positive ion sheath may be required to draw extra current out of the plasma. This is the case shown in the figure. The extra ions required are made in the anode glow, while little excitation occurs near the anode, making a dark space. What happens at the anode is variable, and depends on the details of the individual discharge.

The diagram is slightly different than the one that appears in many references, which seems to be copied from an original by Loeb. The common diagram has, I believe, some inaccuracies, the most important of which is the positive ion density in front of the cathode, which cannot fall to zero, as Loeb seems to indicate, but must remain finite.

We should now discuss the important property of similitude in gas discharges. This rests essentially on the fact that the mean free path is given by L = 1/nπd², where n is the particle density and πd² is an effective cross section for collision. The diameter of an equivalent sphere is d. This expression may be multiplied by a constant near unity to account for a difference in speed of the colliding particles, or the distribution of molecular relative velocities, but the essential thing is the proportionality to 1/n, which holds very well for the dilute gases important in discharges. The number density, in turn, is given by n = p/kT in terms of the pressure and temperature.

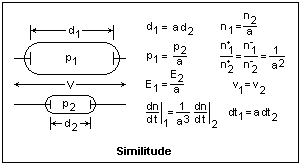We have already seen this in Paschen's Law. The product pd = pL(d/L), in which pL is a constant, and the ratio d/L determines the nature of the discharge, so the same things happen for the same values of pd. The diagram at the right shows two discharge tubes of similar shape, in which the linear dimensions are in the ratio a. The potential difference across the tubes is the same. If the pressures scale in the inverse ratio a, then the number of mean free paths in any similar distances is the same, and pd is a constant for similar behavior. Since the potential difference is constant, the electric fields E = -dV/dx also scale with the pressures, so that the ratio E/p is constant. The ratio α/p is a function of E/p only, so it is constant. From the expression for the currents in the Townsend region, we find that the current densities are constant if the initial current densities at the cathodes are the same. Note that the ratios of charged particle densities are not the same as the ratio of neutral molecule densities. Neutral molecule densities are determined by p = nkT, but charged particle densities are determined by Poisson's equation d²V/dx² = -4πn^±. Rates of change of particle densities are also in a different ratio. Not everything scales properly, but in most cases similitude is a very good approximation. This shows, incidentally, that tests at reduced voltage cannot be made on models, since the discharges will not be comparable if the voltages are different.

Most of the voltage between anode and cathode is represented by the cathode fall V_c near the cathode. Aston found experimentally that the electric field is greatest at the cathode, and falls linearly to zero at the end of the cathode fall in the negative glow. This linear decrease means that the potential rises parabolically: V(x) = (2V_c/d²)x(x - 2d). This means that there is a constant positive space charge in the region of amount V_c/2πd², and the field at the cathode is E_o = 2V_c/d. If K is the mobility of the positive ions, then the positive ion current can be found. The electron current is γ times this, so the total current density at the cathode is j_o = V_c²K(1 + γ)/πd³.

The electrons are accelerated by the strong field near the cathode to a rather high energy. They are then moving much faster than their mobility in the electric field, but are not slowed down much by elastic collisions with neutral atoms, and continue to ionize with increasing efficiency as they slow, doing the most work in the negative glow. The appearance of the spectrum of ionized atoms as well as neutral shows that the electrons still have high speeds in this area, though they are moving in random directions. The width of the negative glow is approximately equal to the "range" of the electrons at the prevailing pressure. This range is not exactly the same as the concept of the same name in the stopping of radioactive beta rays.

It may be naively believed that the electrons are accelerated in the cathode drop as if in a vacuum, and then start ionizing when they reach sufficient energy, but this is not a valid picture, and leads to confusion when trying to understand the discharge. The mean free path is still short even at 1 mmHg, and neutral molecules far outnumber electrons and ions. While the neutral density is about 4 x 10¹⁵ cm^-3 at 1 mmHg, the electron and ion densities do not exceed 10¹⁰, and are usually no greater than 10⁸. Only one in ten million molecules is ionized, and the motion of electrons and ions is governed by mobility rather than by free acceleration. The electron mean free path in neon at 1 mmHg is about 0.5 mm, which does give the electrons considerable freedom to roam. It is no wonder that the cathode phenomena hug the cathode tightly at higher pressures, and expand as the electron range increases. A very high electric field at the surface of the cathode is a feature of all discharges, and here is where the electrons get their initial energy.

Only a few of the necessary positive ions are created in the cathode dark space, where most of the potential rise takes place. Most appear in the negative glow where ionization is most effective, then drift towards the cathode. The range of a fast charged particle is familiar from radioactivity. It is the projected distance in the general direction of motion, not the actual path length, especially for electrons, and is the distance to the point where the particles have insufficient energy for further ionization. The range of electrons of U eV energy in a gas of molecular weight M is about R = 1.4 x 10^-7 (TU²/pM) cm, where p is in mmHg, and T is in K. The negative glow grades into the Faraday dark space as the electrons become relatively slow and unable to ionize. Now they simply have to make their way to the anode somehow without using up much voltage.

The distribution of light intensity in the cathode dark space and the negative glow is a good subject for contemplation. The light does not come from the positive ions (unless they have been further excited, which does happen), but from ions that have recombined. The entire region between the cathode and the Faraday dark space is full of positive ions, but recombination is more likely where the electrons are moving slowly, and this means electrons that have already ionized and are now drifting about, and slower ions that have not yet been accelerated by the field. Electrons in the dark space are still moving too rapidly for this, so there is little light there.

Analysis shows that the cathode fall where the current density required is not too high is V = (3B/A)ln(1 + 1/γ), the current density is j = 5.92 x 10^-8(AB²)(Kp)(1 + γ)p²/ln(1 + 1/γ), in μA/cm² and where the various constants have their usual units, and the width of the cathode dark space is d = 3.76 ln(1 + 1/&gamma:)/Ap cm. These equations can be used to find empirical values for the constants A and B. For neon, K = 7.52 x 10³ cm/s/V/cm at 1 mmHg, and γ = 0.022 on an iron cathode. Experiment gives d = 0.72 cm at 1 mmHg, j = 6 μA/cm², and V = 150V. From these data, A = 20 and B = 261, which is not unreasonable. Note that V is independent of the pressure, d varies inversely with the pressure, and j is proportional to the square of the pressure. This applies, of course, in the range of pressures where the approximate analysis is valid.

The current through a glow discharge is controlled by the external circuit. If a current i is demanded, then a cathode area A = i/j is necessary under the conditions of our analysis. If this cathode area is not available, then the cathode fall must increase to provide a greater current density. This region is called the abnormal glow. The increased cathode fall generates faster electrons and faster ions, so the negative glow expands and brightens, and the fast ions bombard the cathode. In a glow lamp, it is easy to see the negative glow spread as the current through the lamp is increased.

Fast ion bombardment causes sputtering of the cathode material. The rate of sputtering is proportional to (V_c - V), where V is the normal cathode fall, and V_c the established cathode fall. 850V would not be an unusual figure, where V = 200V, say. The exact mechanism of sputtering is in doubt, but it seems that cathode material is ejected to the cathode surface, and then evaporated by the local heating. The rate of deposition obeys the inverse-square law. The films produced are quite coherent and uniform. Silver sputters relatively easily, aluminum with difficulty. Where cathode surfaces are specially prepared, perhaps with low-work function substances as in thermionic cathodes, sputtering can destroy them quickly, even at relatively low overvoltages. There seems to be little sputtering at the normal cathode fall. The electrodes of glow lamps are treated with low-work-function materials, so they are injured by overcurrent, and their striking voltages may rise.

In the Faraday dark space, the electric field is again controlled by space charge and the mean free path, this time of the electrons, which carry nearly all of the current. The kinetic energy gained in a mean free path L is mv²/2 = EeL, so we can find the velocity and hence the current density, j = ne(2EeL/m)^1/2. Then Poisson's equation is dE/dx = 4πne = 4πj(2EeL/m)^-1/2. Integrating this equation, we find that E = (6πj)^3/2(2eL/m)^-1/3x^2/3. Hence, the electric field rises as we move through the Faraday dark space. When it reaches a value sufficient to give the electron a kinetic energy equal to the resonance energy V_r, then the electrons can excite the neutral molecules and light emission begins. This happens in a distance x at which EL = V_r, which is proportional to 1/Lj, or inversely proportional to p. If the pressure is sufficiently low, then the electrons move almost as in a vacuum, and the normal Childs 3/2-power law applies. Then the distance x is proportional to 1/√j, again inversely proportional to pressure. Like the cathode fall and the negative glow, the Faraday dark space also expands inversely as the pressure. Therefore, the whole cathode region expands or contracts without any change in relative dimensions as the pressure changes.

When the average electron has sufficient energy to excite a neutral molecule to its resonance level, the occasional overzealous electron can ionize a molecule to create a positive ion to replace one that is lost by diffusion to the wall, where it recombines. This is a delicate balance that keeps electron and ion densities equal in the positive column or plasma. The smaller the diameter of the tube, the greater is the diffusion, and the greater the longitudinal potential gradient required to keep the electrons up to working speed. The random current density is the current crossing unit area in one direction in the plasma, j = nec/4, where c is the average thermal velocity of the charge carrier, √(8kT/πM). This presumes a Maxwellian distribution, which is not a bad assumption. However, the electron temperature may be 10,000K or more while the neutral and ion temperatures are not much above 300K. This difference is due to the extreme difficulty of transferring kinetic energy between the light electrons and the heavy molecules, especially when the electrons are being driven by a longitudinal field. This means that the random electron current to the wall is much greater than the random ion current. So that the net current to the nonconducting wall is zero, the wall must collect electrons to form a repelling field. This layer of excess charge is called a plasma sheath, and is a common phenomenon, well seen in glow discharges.

For a neon glow discharge carrying 25 mA, the voltage gradient in the positive column for a tube radius R = 2 cm is 1.45 V/cm. For R = 1 cm, it is 3.0 V/cm, and for R = 0.75 cm it is 4.3 V/cm. For helium, the drop in a tube of 1.5 cm radius is 5.0 V/cm. A neon display lamp uses the positive column for its light. The tube diameter may be 0.6" diameter and its length 60 ft. The total drop in the positive column is 130 V/ft x 60 ft = 7.8kV, and the electrode drops amount to 230-300V. The illumination is about 36 lumen/ft, and the efficiency 24 lm/W. On open circuit, the transformer supplies 15kV. However, it is made with large leakage reactance that lowers the voltage depending on the current drawn to stabilize the discharge at something less than 10kV across the tube. The pressure in the tube is larger than the value giving minimum voltage to suppress sputtering of the cathode, which darkens the walls of the tubes and limits the life of the tube. Neon gives red-orange, helium yellow, nitrogen pink. Mercury can be added for further colors, and colored glass can be used, to make blue and green displays. These glow discharges are still a frequent sight.

Corona is the name given to glow discharges at high pressure near points of high fields, usually caused by a small radius of curvature. Points are an obvious place for corona, and this is their intention in lightning rods. High tension conductors are another good place, but here it is very undesirable. It is commonly stated that the breakdown field for air is 30kV/cm, but the phenomenon is far too complex for such a simple criterion. Nevertheless, this value is of use for engineering estimates. A negative wire becomes a cathode, and the glows contract to regular regions along the wire, like beads, each surrounded by a brush. A positive wire becomes an anode, with a uniform anode glow spread along it. Corona loss may exceed resistive loss in the conductors. It is less if the conductors are smooth and of large diameter.

The glow discharge is often used for gas laser pumping, as in the familiar He-Ne laser. The object is to create a population inversion between the upper and lower levels of a radiative transition. The upper level for the 633 nm laser transition is the Ne2p⁵5s'[1/2]₀ at 166658.484 cm^-1 above the Ne ground state, which is nearly resonant with the He2¹S₀ metastable excited state of helium, and the lower state is the Ne2p⁵3p'[3/2]₂ state at 150860.468 cm^-1, which can decay rapidly to the Ne2p53s[3/2]₂ metastable state of neon via 594.5 nm radiation, keeping the lower state empty. This is a very fortunate and ideal scheme for laser pumping. There are also infrared transitions in the same region that can be used, at 1152 nm and 3391 nm. The upper level of the first is resonant with the metastable He2³S₁ state, which also facilitates pumping.

The discharge tube is typically filled with 0.8 mmHg helium and 0.1 mmHg neon, excited by a dc discharge, an ac discharge, or radio-frequency discharge. The population inversion is in the pink positive column. The laser frequency is picked out by an optical resonance between external mirrors, and energy is pumped into it by the population inversion. The cathode and anode are usually in side tubes so the optical path is not obstructed.

A radio-frequency field from an external coil around the discharge tube can be used to create a plasma. It is necessary for the rf electric field to be strong enough to give the excitation or ionization energy to an electron in a mean free path. This is not strictly a discharge, since there is no net current flow, but it produces a weakly-ionized plasma like that in the positive column of a glow discharge.

As the gas pressure is reduced, it becomes more and more difficult to produce a sufficient number of positive ions to maintain the discharge. The anode-to-cathode voltage must be continually increased, and the electrons become more and more energetic. The electron mean free path becomes comparable to the size of the discharge, and practically the whole space represents the Faraday dark space. This is the region of cathode rays, as the linear electron trajectories were called before electrons were recognized, that can cast shadows, deflect in transverse electric and magnetic fields, cause the glass to fluoresce, and produce X-rays when they are stopped suddenly by the anode or the glass. Finally, the tube becomes nonconducting.

The arc discharge is a high-current, low-voltage discharge, in contrast with the low-current, high-voltage glow discharge. It is characterized by a negative-resistance V-I characteristic, and high temperatures. Electrons for the discharge are supplied by a cathode spot that is a much more efficient electron emitter than the glow discharge cathode phenomena. The current density in the cathode spot is high and constant, so it adjusts its size to suit the discharge current. The electrons are liberated either by thermionic emission, or by high-field emission. The relative importance of these mechanisms has long been in dispute, but it is convenient to assume that the fixed cathode spot of refractory electrodes (such as carbon or tungsten) is thermionic, while the wandering cathode spot of low-melting-point cathodes (such as mercury) is high-field. A typical current density for a thermionic cathode spot is 470 A/cm², and of a high-field spot, 4000 A/cm².

High-field emission is essentially quantum-mechanical tunneling through the potential barrier at the surface of the cathode. The current density is given by the Fowler-Nordheim equation J = CE²exp(-D/E), where C = [6.2 x 10^-6/(φ + E_F)](E_F/φ)^1/2 A/V², and D = 6.8 x 10⁹φ^3/2 V/m. E_F is the Fermi energy and φ is the work function, both in volts. E is the field in V/m. For tungsten, φ = 4.52V and E_F = 8.95V. The fields required are very high. A field of 2 x 10⁷ V/cm produces emission of only 1.7 μA/cm² in tungsten. However, the current increases quite rapidly with electric field. With a field of 3 x 10⁷ V/cm, the current is already 0.2 A/cm². At atmospheric pressure, the mean free path is about 10^-5 cm in air, and if the cathode drop is 10V, the resulting electric field if the cathode drop occurs over one mean free path is 10⁶ V/cm. This is about a factor of 20 less than is required, so some investigators have questioned the importance of high-field emission in arcs. However, it is at least close to the required value, and some local strengthening of the field by the arrangment of adsorbed positive ions may make up the difference.

The Richardson-Dushman equation for thermionic emission, J = AT²exp(-b/T) is very similar in form to the Fowler-Nordheim equation, with the absolute temperature T replacing the field strength E. A = 60.2 A/cm², and b = 11600φ. At the boiling point of tungsten, 5993K, J = 3.45 x 10⁵ A/cm², a quite ample result. Even at the melting point, the current density is 541 A/cm². Mercury has about the same work function as tungsten, 4.5V, but the thermionic emission at its boiling point, 630K, is only about 10^-29 A/cm², which is wholly inadequate. Therefore, high-field emission seems to be the only alternative.

A typical low-intensity carbon arc for lighting operates at atmospheric pressure between two cylindrical carbon electrodes separated by a few millimeters, at a voltage of 55V and a current of 30A. The cathode spot is at a temperature of about 3500K, while the crater eroded in the anode carbon is around 4200K, with a brilliance of 170 cp/mm². Between them is a bright violet glow, and a yellow tail flame, projected towards the anode. Material is blown out by the cathode, and may deposit on the tip of the anode. The light is characteristic of a 3810K black-body, with strong radiation in the near UV at 380-390 nm, the cyanogen peaks due to that compound of carbon and nitrogen. There is also a peak near 250 nm. These ultraviolet emissions make protective glasses necessary when observing an arc directly. The radiation is also rich in infrared, because of all the heat in the vicinity.

The carbons are continually consumed in the arc. They may be of hard carbon for durability outside, with a core of soft carbon for conductivity inside, that stabilizes the arc. Special core materials may give colored arcs by coloring the tail flame. They cannot be focused accurately as the postive crater can. A core of cerium oxide and cerium fluoride forms cerium carbide in the crater, giving up to 500 cp/mm² in what is called a high-intensity arc light. The tail flame is white from the incandescent cerium particles. A typical positive carbon is 16 mm in diameter, with an 8 mm core, while the negative carbon is 11 mm in diameter, with a 3 mm soft carbon core.

The arc can operate either in the ambient gas, or in the vapor emitted by the cathode and anode as they are vaporized. The electrodes operate at their boiling points, which determines the maximum temperatures available. For example, a copper arc is typically green, with emission from the copper vapor in the arc. The arc consists of the cathode drop, the positive column, and the anode drop. No interesting detailed structure is seen, as in the glow discharge. The cathode drop is a little less than the ionizing potential of the gas or vapor. For carbon, the ionization potential is 15.8V, but the cathode drop is 9-11V. The width of the cathode drop region is little longer than a mean free path of an electron, so the cathode region is very thin. The anode drop occurs in a wider region, and resembles a probe sheath, as in a glow discharge. The anode drop in the carbon arc is about 20V. Between the narrow cathode and anode regions is the positive column with a linear voltage gradient. The voltage of a carbon arc in air is given approximately by V = 38.9 + 2.0x + (16.6 + 10.5x)/I, where V is in volts, I in amperes, and x is the arc length in millimeters. This applies in the silent region where the characteristic is hyperbolic. At higher currents, the arc becomes a hissing arc, and the voltage is roughly constant.

Thermal effects play an important role in arcs. The cathode is heated by positive ion bombardment, where the effect of the ions is purely thermal and any positive-ion induced electron emission is unimportant. There must always be sufficient ions to keep the cathode hot. Often the cathode is externally heated, at least until the arc is established, to help starting. This is seen, for example, in fluorescent tubes. In some cases, as in rectifier gas diodes, the cathode is continuously heated. These cathodes are oxide-coated to stimulate copious electron emission. External heating of the cathode does not affect the nature of the discharge significantly. By considering the positive-ion space charge, the field at the surface of the cathode can be estimated as E = 4V/3d, where V is the cathode drop and d is the width of the cathode fall region. If V is about 10V and d is about a mean free path, then E is 10⁵ to 10⁶ V/cm. Such a high field is great encouragement for electrons to join the discharge. Also, a superheated area may form at the surface of the cathode from adsorbed atoms.

The positive column differs significantly between arcs operated at low pressures (say, below 10 cmHg pressure) and arcs at higher pressures, such as atmospheric. At low pressures, it is like the positive column of a glow discharge, with a very high electron temperature (40,000K is not unusual) and a low ion and gas temperature (say, 300K). Ionization in this plasma is by electron impact, and the plasma dissipates if the walls are not present. At high pressures, electron, ion and gas temperatures are equal and high (perhaps 6000K), and ionization is principally thermal. This is the kind of hot plasma studied in plasma physics. The longitudinal voltage gradient depends on current as E = BI^-n and on pressure as E = Cp^m, where m and n are empirical exponents. For a carbon arc in air, n = 1 and m = 0.3, approximately. At 1 atm, the current density in a positive column in nitrogen is about 6 A/cm². The reason for the decrease in voltage with an increase in current is that the current increase causes a decrease in the resistance of the column by making more of everything available.

The degree of ionization x in a hot plasma can be estimated by the Saha equation, [x²/(1 - x²)]p = 3.16 x 10^-7 T^5/4exp(-eV_i/kT), where p is in atmospheres, T is in K, and V_i is in volts. If we take an ionization potential of 10V (about that of mercury), then at 10,000K and 1 mmHg the Saha equation gives x = .033, or the plasma is about 3% ionized. At 100,000K, the degree of ionization is x = 0.997, so the plasma is almost completely ionized. Even at 1 atm, the degree of ionization is still about 41% at 10⁵K and 0.1% at 10⁴ K. A fairly small degree of ionization suffices to maintain the conductivity of a high-pressure arc plasma.

In hot plasmas, oxygen and nitrogen are generally dissociated: O₂ → 2O (5.09 V) and N₂ → 2N (7.9 V), and the reaction N₂ + O₂ → 2NO. NO has the rather low ionization potential of 9.5V. The ionization potential of O₂ = 12.2V, O = 13.614V, N = 14.54V, N₂ = 15.377V. Even when the electron and ion number densities and temperatures are roughly equal, electrons still carry the preponderance of the current because of their higher mobility.

The high-pressure positive column adjusts to a finite diameter D depending on the discharge current. It will not expand indefinitely if unconfined. This is a result of a delicate balance between heat loss and heat generation in the conducting region, and not anything similar to a "pinch" effect. If the column expands, heat loss increases and ionization decreases. The current, therefore, tends to shift to the more conductive center, and raises the temperature there. This feedback keeps the column at a constant diameter. The positive column is a cylindrical region in the ambient gas, and can move about freely, so long as it does not become too long and require more voltage than is available. It is accompanied by active convection that carries off its heat. The positive column can be blown about by air currents, and moved by magnetic forces. Its low density causes it to rise when surrounded by cooler air, which, as we have mentioned, gave the name "arc" to the phenomenon. Curiously, if the acceleration of gravity is zero (as in a space station, for example) the longitudinal voltage gradient becomes zero! The reason is that gravity drives convection, and in the absence of convection the column does not cool, and so does not need any power, at least to a good approximation. Note that this means that the whole arc, including the gas, is under zero gravity. If we just let the electrodes fall, it is only like applying a blast of air.

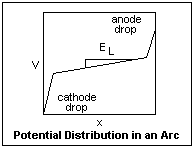The potential distribution in an arc is shown at left. The widths of the cathode and anode drops are exaggerated for clarity. In a short arc, the potential is almost just the sum of the cathode and anode drops. Because of the large current, an arc has a small longitudinal voltage gradient E_L in the positive column, especially in a high-pressure arc. The gradient depends on the efficiency of cooling of the positive column by the ambient atmosphere, and becomes small if cooling is slow. The current flowing through the cathode and anode drops generate large quantities of heat very close to the electrodes, which is one of the characteristics of the arc.

An arc can be started either by a transition from a glow discharge, or by separating contacts already carrying current. If we increase the current in a glow discharge, we enter a region in which the width of the cathode fall decreases (the "abnormal glow"). This causes the ion energy to increase, and the cathode becomes heated. In arcs with thermionic cathodes, the transition is gradual as the thermionic emission increases with temperature and the discharge voltage decreases. With field-emission cathodes, such as with mercury, the transition may be sudden, as a cathode spot is created at some favorable spot. The mercury is initially in liquid form, either as a pool or as a drop, and must be raised to a temperature where the mercury vapor pressure will support the discharge. Starting a mercury arc always requires some special action, either a separately heated cathode or an ignition electrode. The pressure can also be increased to start an arc if a glow discharge already exists. The current rises as the square of the pressure, so a critical value is soon reached.

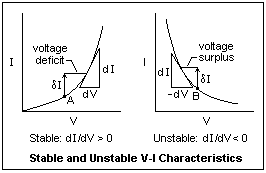The distinction between stable and unstable V-I characteristics is shown in the diagram at the right. On the left we have the usual case where the current increases monotonically with the voltage, so that the slope 1/R = dI/dV is positive. Suppose we are operating at point A with a certain applied voltage, and there is a sudden increase in the current δI (caused, say, by a spark). Now the voltage required by the device is greater, so we have a voltage deficit in the circuit that will cause the current to decrease. If the current were suddenly less, then we would have a voltage surplus, and the current would be driven to increase. In either case, we return to the status quo and the circuit is stable.

On the right, we have a characteristic like than of an arc, where the current decreases monotonically with the voltage. The slope 1/R = dI/dV is now negative. The device is said to exhibit negative resistance R. If we have a sudden current increase δI from point B, then we have more voltage available to increase the current still more, a voltage surplus. The more the current increases, the more it is driven to increase. The circuit is unstable, and some external means is necessary to limit the current. Any device with a negative resistance can be used as an oscillator, and an arc is no exception.

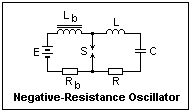A negative-resistance oscillator using an arc is shown at the left. It should not be confused with the spark-gap oscillating circuits used in early radio, which were something completely different. L and C make a tuned circuit in series with the arc, and R is the resistance of L. The arc is supplied from source E through a large inductance L_b that blocks the oscillating current and keeps the arc voltage constant. The arc current is regulated by resistance R_b. Kirchhoff's voltage law around the loop including the arc, L, C and R gives Li" + (R + de/di)i' + i/C = 0. If the arc current is adjusted so that de/di = -R, then we have Li" + i/C = 0, so that the solution for i is a harmonic function of frequency f = 1/2&pi√LC. Since de/di is a function of the current, large current excursions will be damped out and the amplitude of the oscillation will stabilize. The maximum voltage across the capacitor will be I√(L/C), where I is the arc current. I do not know of any practical use of this oscillator, but the oscillations may occur unexpectedly in some cases.

Welding is an important application for arcs. Although oxyacetylene flames are hot enough to make fusion welds and are very useful, arc welding is relied upon for heavy-duty welding. In carbon-arc welding, the arc is struck between a carbon rod and the work, and a filler rod is used if extra material is needed. Inert-gas welding uses a tungsten electrode bathed in an inert gas such as helium to avoid oxidizing the work, and a filler rod. Argon is also used, though one source says it is not suitable. Since helium, and even argon, are quite expensive, welding with CO₂ has also been tried with success. Atomic-hydrogen welding uses a pair of tungsten electrodes between which the arc is struck. Hydrogen is blown onto the arc, where it dissociates. The atomic hydrogen then recombines on the surface of the work, creating the necessary high temperature. These methods are useful in special cases, but the most general type of arc welding is the metallic arc. The arc is struck between a welding rod and the work, with the welding rod providing the filler metal.

It is necessary to exclude the oxidizing atmosphere from the molten metal in any welding, and this is done by the gases created from the coating of the welding rod. This coating also provides material that makes a slag that carries away impurities and is brushed off the surface when it is cool. Special alloys in the welding rods provide additions necessary for the quality of the weld material. The selection of the proper welding rod is an important requirement for successful welding. The blast from the cathode when the welding rod is made negative and DC is used allows overhead welding, a great advantage of metallic arc welding, though it is not used except when absolutely necessary. The arc length is short, 4 mm or less, the coating generally touching the work as the weld is made. A voltage of 21V and currents of 40 to 240A are typical. A generator for DC welding supplies 40-60V on open circuit, but is strongly negative compounded to limit the current to the desired level. A transformer with large leakage flux is used for AC welding, for the same reason. When DC is used, the work is generally positive because of the higher temperature at the anode, but it depends on the welding rod used. Proper welds are strong and reliable, and the ease and economy of making them has led to their general use instead of riveted joints.

The Cooper-Hewitt low-pressure mercury arc lamp is shown at the right. It produced 16 lm/W of the line spectrum of mercury, including the UVA resonance line at 257.3 nm. It was used, among other things, for exposing blueprints and blueline prints (as was the carbon arc). It is interesting for using two anodes for operation on AC, a mercury-pool cathode, and a capacitance igniter. The pressure of mercury in operation was a few mmHg, controlled by the bulb temperature. The discharge current was limited by the ballast L, and the anode currents equalized by the resistances R. The AC supply was arranged as an autotransformer. The capacitance igniter consisted of a ring around the bulb at the level of the mercury surface. When the switch was closed (this switch was a mercury tilt switch) DC passed through L, so that opening the switch produced a large inductive kick that was applied to the ring through the capacitance C. This apparently created high-field emission at the mercury meniscus inside the bulb, which started the discharge. Residual ionization was enough to restart the discharge on each voltage cycle.

Starting a discharge with a mercury-pool cathode means establishing a cathode spot on the surface of the mercury. This could be done with a small auxiliary pool that was connected to anode potential and then tilted to separate the mercury from the main cathode, after which the discharge would transfer easily to the main anode. Another method used a resistive rod that was not wet by mercury dipping into the pool, called a resistive igniter. A small auxilary anode, called an arc-holding anode, was sometimes provided to keep the discharge going when the main anode current was cut off, perhaps by some current control action. The capacitance igniter eliminated the inconvenience of a conductive connection to the discharge, simplifying control.

The cathode spot makes a small depression in the surface that moves about rapidly, with agitation and splashing of the mercury. Mercury is vaporized at the cathode spot, and condenses on the cooler parts of the envelope, from where it drains back into the pool. This self-renewing property of the mercury pool cathode is a great advantage. However, the mercury must not splash on an anode, where it offers the hazard of creating a secondary cathode that may conduct on reverse voltage, causing a backfire.

Large mercury-pool rectifiers were once used to produce large DC currents. The ignitron even allowed phase control. These rectifiers have now been superseded by silicon rectifiers, which are much cheaper and more convenient to use, but much less dramatic.

The sodium-vapor lamp is another interesting device. It was necessary to find a glass that would not be attacked by hot sodium vapor before any such lamp was possible. The lamp uses a separately-heated oxide-coated cathode and a molybdenum anode in about 2 mmHg of neon. The discharge is first started in the neon, and the lamp allowed to warm up until the sodium metal vaporizes. This requires up to 10 minutes. Sodium melts at about 93°C, and at the working temperature of 220°C has a vapor pressure of about 0.3 μmHg. A Dewar enclosure around the envelope keeps the heat in. This is a small pressure, but the efficiency of radiation of the sodium resonance lines is so great that most of the light comes from the sodium. A short lamp, 8 cm, relies on cathode phenomena and has no positive column. Its voltage drop is about 17V, and it produces 4000 lm, for an efficiency of about 22 lm/W. A longer 16 cm lamp will get its light from the positive column, and the voltage drop will be about 25V. This lamp will produce 7000 lm, with an arc efficiency of 72 lm/W, and an overall efficiency of 52 lm/W, the highest known. The light, however, is monochromatic, in the range 560-610 nm, formed by the broadened sodium D lines. This orange-yellow light was once very familiar as highway illumination.

The neon in the lamp, though it does not contribute to the light, has the important function of decreasing the electron mean free path so that the electrons spend a lot of time in the discharge, and have a high probability of exciting sodium atoms. The cathode fall of the lamp is about 15V, low enough that ion bombardment of the cathode is not damaging (this happens at 25V and above). The cathode fall is set by the neon, but the resonance energy of the sodium is only 2.5V, allowing nearly all the sodium to be excited. The electron temperature in the positive column is about 40,000K. The voltage gradient is small because the neon can be cumulatively ionized, since it has metastable levels and can save excitation energy between successive collisions with electrons. The number density of sodium in cm^-3, is given in terms of the temperature T in K by log n = -5573.3/T - 1.6794 log T + 28.7134. When the walls are at 390K, this gives 5 x 10¹⁰cm³. At these temperatures, the resonance radiation has an absorption coefficient of 143 cm^-1, so it does not get far before it is absorbed and then re-radiated. Only a thin outer skin of the positive column emits the light that is seen.

High-pressure sodium lamps have now been developed, in which the high pressure produces a very hot plasma that radiates throughout the visble, making a golden light that is more acceptable than the pure yellow of the low-pressure lamp. They are widely used as streetlights, giving an annoyingly bright glare. It is interesting to watch these lamps light with a spectroscope. When they first are connected, they show argon or neon lines, then the blue of a mercury discharge and its typical yellow, green and red lines. The sodium D lines soon appear, and they increase in brightness, and then in width. Finally, when the lamp is at operating temperature, there are two black lines against the continuous background, as the sodium vapor absorbs these frequencies, that by contrast look dark. This is similar to the production of the Fraunhofer dark lines in the solar spectrum by line absorption of the photospheric continuum in the chromosphere.

The high-pressure mercury arc lamp was developed earlier than the high-pressure sodium lamp, since the problems with its construction were not as challenging. It is filled with argon to a few mmHg, and contains a small mercury drop, perhaps 200 mg in weight, that will supply the operating pressure in a tube 15 cm long and 3 cm in diameter. The operating wall temperature is about 350°C. A glow discharge at the starting electrode close to one main electrode provides sufficient ionization for a glow discharge to begin between the main electrodes, which raises the wall temperature. When the mercury is vaporized, the arc strikes, and the oxide-coated cathodes are heated by ion bombardment. The lamp is supplied through a transformer with leakage flux, so that it behaves as a ballast as well. The inductive current is balanced by a capacitive current to correct the power factor, if this is a problem. These lamps produce a whitish-blue light from the broadened spectral lines of mercury, which at the highest pressures becomes practically a continuum.

The fluorescent lamp is a very familiar device, that provides us with examples of a low-pressure mercury arc, and an argon glow discharge as well. The tube, which is from 5/8" to 1.5" in diameter, and 9" to 48" long, has an oxide-coated cathode with heater at each end. The 253.7 nm mercury resonance line is ideal for exciting phosphors such as manganese-activated zinc silicate. This phosphor has an excitation peak at 253 nm, and re-emits the radiation in the region 460-600 nm in the middle of the visible spectrum. There are many phosphors to choose from, and combinations of them are used to secure desirable spectral characteristics. They operate at rather low currents, 0.15 to 0.42 A, and at voltages from 45V for a 9" tube to 108V for a 48" tube. A ballast inductor is used to limit the current. A resistor would work as well to limit the current, but the inductor dissipates less heat, though at the expense of a poor power factor. The inductor, however, plays an important role in starting the discharge.

Since the tube contains a drop of mercury that must be vaporized before the dicharge can start, the cathode heaters are connected in series across the line to warm up the mercury and provide some ionization. When the starting switch is opened, the inductor gives a high-voltage kick that initiates the arc, though it may be a while before the tube comes up to operating temperature. Fluorescent lamps are very efficient, a green phosphor giving as much as 70 lm/W, though normal lamps are less efficient. There is little infrared in the radiation produced. The visible mercury lines shine through the phosphors, and can be seen in a spectroscope. The light is not very pleasant, but gives good illumination of large areas.

The "glow switch," an automatic starter, was invented by R. F. Hays in 1940. It has a U-shaped bimetallic strip that closes the circuit through the lamp heaters when it is hot, but the contacts are normally open. There is another electrode in the envelope so that a glow discharge can occur when voltage is applied. The normal supply voltage is enough to start the discharge, which is in the abnormal glow region to supply a good amount of heat to one end of the bimetallic strip. The strip closes the contacts and shorts out the glow discharge, and the tube heaters are energized. It is arranged that the bimetallic strip continues to heat a short time after the discharge ceases, so the circuit does not reopen immediately. When the bimetallic strip cools the contacts open, causing the inductive kick that starts the main discharge, as well as the glow discharge in the starter. However, the voltage across the main discharge is insufficient to maintain the glow discharge, so the glow discharge goes out before it can heat the bimetallic strip again. If the main lamp does not light, the cycle repeats until it does. These starters are practically universally used, and may be included as part of the lamp.

Arcs are also involved in power switching. The ordinary AC houshold supply is one of the easiest circuits to switch. A DC supply, even of the same voltage, is much more difficult to interrupt. A switch that can handle 10A AC will do well to handle 1A DC at the same voltage. High-voltage transmission circuits are very difficult to switch, even with AC, and a large amount of technology has been developed to meet the problems. When a circuit carrying current is interrupted, an arc always forms at the switch contacts, and the arc must be lengthened until the voltage will not support it. Inductance in the circuit always makes switching more difficult. Care must be taken not to end the current abruptly and cause an excessive inductive kick, while the inductance extends the persistence of current flow. Alternating current has the great advantage that the current is zero twice in every cycle, and advantage can be taken of this to break the circuit. DC of several thousand volts is very difficult to interrupt, since the voltage can support a long arc that must be extinguished in creative ways. Opening a simple knife switch would only result in a continuous arc in this case.

The arc can extend itself by climbing arc horns driven by its buoyancy and convection of the air around it, or the current can be used to create a magnetic field with the same effect, called a magnetic blowout. The arc can be driven into an arc chute that lengthens its path, by a blast of air. In the most difficult cases, the contacts open in an oil bath. This creates a cloud of vapor under high pressure that may be used to blow out the arc, and occasionally a nasty explosion. A great deal of ingenuity has gone into high-voltage switchgear to make economical high transmission voltages practical. However, one supposes a high-voltage DC transmission line cannot be switched at all, and its supply must be removed instead, or it simply must be shorted.

Lightning offers further problems. Here, the voltages can rise to several million volts in a few microseconds, with currents of thousands of amperes. Lightning protection must allow a discharge that bypasses equipment that would be damaged by the stroke. Here we are talking about actual lightning strikes, not just disturbances due to nearby lightning that affect telephone wires and such. The protection that routes a stroke around an insulator may leave ionization that facilitates an arc over the insulator from the normal line voltage, damaging the insulator, so protection equipment must work quickly to de-energize the line when a lightning stroke is detected. When your lights flicker briefly, the usual reason is that a lightning strike has caused the protective circuits to disconnect and reconnect the line automatically. This is just a sample of the many problems that occur in this field.

Even voltages as low as 1.5V can cause a "spark" when contacts open. This is not a true spark, but the effect of high temperatures produced at the last point on the contacts to open, when the current is confined to a small area. This is not a switching hazard, but does degrade the contacts. A capacitor can be used to keep the voltage across opening contacts small, but a resistor is necessary in series with it. Otherwise, when the circuit is closed, the voltage across the charged capacitor would be discharged through the low resistance of the contacts, which could weld them together. This combination is called a snubber, and it makes low-voltage DC switching a little better.

Fuses are an excellent overcurrent protection. They consist of a wire or equivalent that melts at a current that is greater than the working current by some small factor, say 1.5. When the wire melts, an arc is formed that then must be extinguished, often by being enclosed in some material that vaporizes and blows out the arc, or absorbs the energy of the arc. The current that melts a wire can be estimated by Preece's formula, I = Ad^3/2, where I is in ampere and d is in inches. For copper, A = 10,224, for aluminum, A = 7585, for lead A = 1379, and for German Silver, A = 5230. A #30 copper wire fuses at a current of about 10A.

More complete bibilographies will be found in the references.

J. D. Cobine, Gaseous Conductors (New York: Dover, 1958).

J. Millman and S. Seely, Electronics (New York: McGraw-Hill, 1951). Chapters 9, 10 and 11.

G. Herzberg, Atomic Spectra and Atomic Structure (New York: Dover, 1944).

Composed by J. B. Calvert
Created 3 November 2002
Last revised 29 September 2005