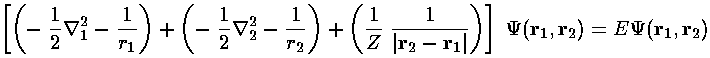
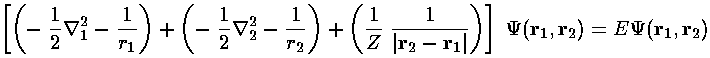
If we ignore the interaction potential (i.e., the term proportional to 1/|r2-r1| ), the Hamiltonian is the sum of two terms, each identical in form to the H-atom Hamiltonian we've already solved, each a function of just one electron's coordinates. Just as in the separation of variables: if the variables in the Hamiltonian can be separated into different terms, we use a product wavefunction to solve the Schrödinger's equation:
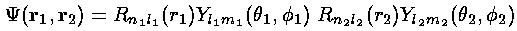
The eigenenergies of this simplified system are just the sum of the 1-electron eigenenergies:
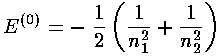
We now include the interaction potential as a perturbation. The first order energy shift is just the expectation value of the perturbation using the unperturbed (simple product) wavefunctions:
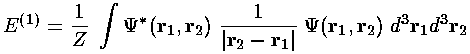
If we slip back into normal (dimensioned) coordinates
we can provide a simple explanation of this term. Electron
1 is distributed in space as given by its wavefunction. Thus there
is a negative charge density surrounding the nucleus:
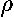=-e|
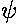|2
where e is the unit charge (i.e., -e is the charge
on an electron). This charge density produces a electrostatic
potential we can calculate (we use here cgs units: no
4
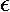0):
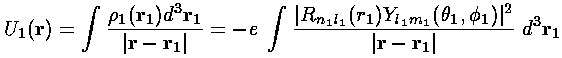
Electron 2 therefore feels, in addition to the the electrostatic potential of the nucleus, the above electrostatic potential. We can calculate this additional energy:
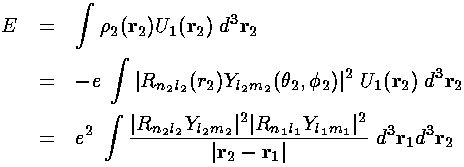
which is exactly the above term (but in dimensioned coordinates).
The fact that the electrons in a multi-electron atom feel the total electrostatic potential due to the total charge: both the attractive nucleus and repulsive electron-cloud, suggests an approximation scheme. As a first approximation solve Schrödinger's equation with just the nuclear potential. Calculate the charge density of the resulting electron clouds and now use the total charge density (nucleus and electron-cloud) to calculate the total electrostatic potential. Use this improved electrostatic potential in Schrödinger's equation; calculate new wavefunctions and electron cloud densities; again calculate an improved electrostatic potential. Continue this process until it become self-consistent, i.e., a new iteration has no noticeable effect of the wavefunctions/eigenenergies. This method is called the self consistent field method or the Hartree method (or Hartree-Fock method, for an improved version accounting for wavefunction symmetry [see below]).
The above interaction integral looks like a mess to evaluate. We proceed by expanding 1/|r2-r1| in terms of spherical harmonics:
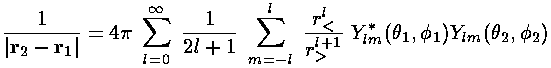
where, r> is the larger of r1 and r2 and r< is the smaller of r1 and r2. With this substitution, the interaction integral become a sum of terms like this:
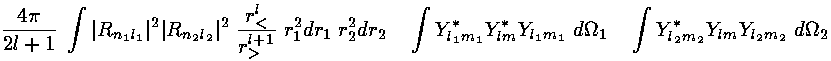
Almost all of these terms are zero because most of the 3-Ylm angular integrals are zero.
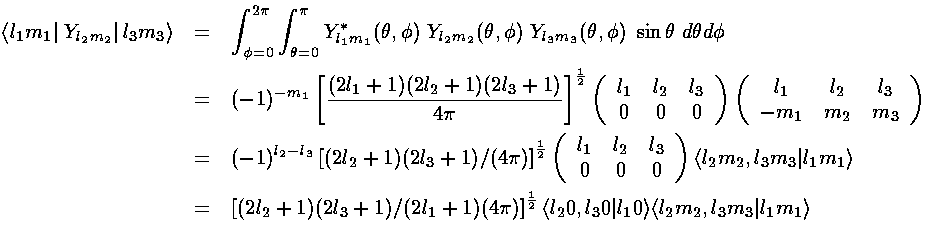
m must be zero for 3-Js to be non-zero.
(This is basically the statement that if the charge density
is 
-symmetric, the resulting potential
must be -symmetric). And
0<=l<=2li. (This is basically
the statement that a charge density going like
|Yl0|2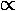 
Pl2
has at most a 2l-multipole.) Further l must be even.
(This is basically the statement that if the charge density is inversion-symmetric,
the potential must be also.)
We pick a particular two electron problem: the first excited state
of helium. Thus electron 1 is in the 1s state
(n1=1, l1=0, m1=0)
and electron 2 is in one of the n2=2 states:
2s or 2p. So l=0 and the sum is just
one term with trivial angular integrals since Y00
is just a constant: 1/(4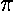)½.
Thus in both 3-Ylm integrals,
Ylm=Y00 is constant and can be pulled
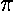from the integral. Since 4|Y00|2=1,
the first-order energy correction is just 1/Z=½ the
radial integral.
We are left doing the radial integral using Mathematica:
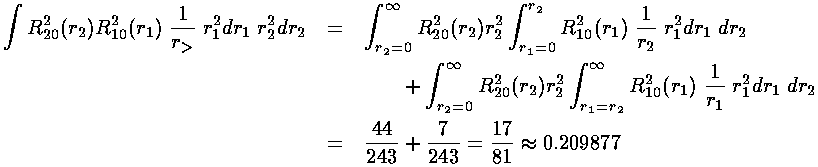
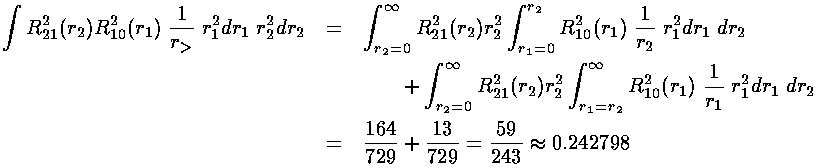
Thus the energy of the 1s2s state is approximately:
-½(1+¼)+½(0.209877)= -.520
Thus the energy of the 1s2p state is approximately:
-½(1+¼)+½(0.242798)= -.504
i.e., the 2p state lies .016×(Z227.2 eV)=1.8 eV above the 2s state. Our 2s-2p splitting is about a factor of two too large. The over all binding energy is fairly close to the approximately (-58 eV)=-.533 seen experimentally--perturbation theory has much improved the initial energy estimate of -.625. The problems at the end of this section describe yet more accurate approximation methods.
The main point here is that the l degeneracy seen in the H-atom [i.e., that all the states with the same principal quantum number n but different values of l (0<=l<=n-1) have the same energy: E'=-½(1/n2)] is broken in multi-electron atoms. The repulsive electrostatic potential of the orbiting electrons changes the potential from an exactly 1/r form to something more complex. As a result the ns state ends up below the np states, which are in turn below the nd states. We call this phenomenon l-tilting. We will see that in many-electron atoms, l-tilting can be so large that the 4s state can be below the 3d state.
Remember that classically the maximum l states (l=n-1) are circular orbits where r=a the semimajor axis, whereas the l=0 orbits range from r=0 to r=2a. Thus the low-l states are both on average are further away from the core electrons (and hence feel a reduced interaction) and occasionally very close to the nucleus (and hence occasionally feel the full nuclear attraction).