Band Structure p.2

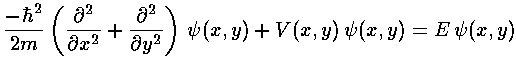
We seek to solve Schrödinger's equation:

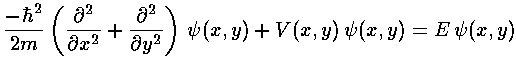
for our array of closely packed attractive potentials. We seek the eigenenergies E and wavefunctions 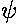that are solutions to the above equation.

While in the end we will be seeking a computational rather than analytical solution to this problem, it is still critical to seek length, energy, etc. scales. Computers may not object to finding, say, cos(x) where x=5 meters, but any result is meaningless. For length the obvious scale is the lattice spacing a. We can then make an energy scale: e=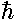²/(ma²) Thus, neglecting to prime our new dimensionless x'=x/a, V'=V/e and E'=E/e, Schrödinger's equation becomes:

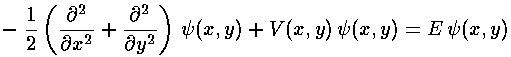
We are aided in solving this equation by the symmetry of the potential. For our 1d lattice of delta functions, Floquet's theorem came to the rescue, allowing us to search for solutions that were "nearly" periodic. This theorem can be generalized to more dimensions, in which case (at least in physics) it is known as Block's theorem. Thus we let:

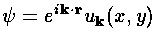
where u_k is a function periodic on the lattice, and k ("crystal momentum") labels different wavefunctions. If we plug this form into our Schrödinger's equation, we find u must satisfy:

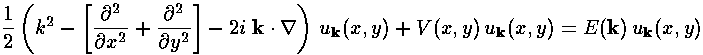
Note that u_k determines the probability density as e^{i k·r} cancels out of ^*.

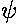Finding E(k) is what we mean by finding the band structure.

We finish with a table showing the typical range of our length and energy scales. Note that none of the below are actual 2d crystals. Since actual 3d crystals often have lattice vectors with unequal lengths, "Lattice Size" may contain several entries.

Solid	Lattice Size (Å)	Energy Unit (eV)	Crystal Structure
Si	5.4	0.26	diamond (FCC), Fd3m
Cu	3.6	0.59	FCC, Fd3m
-Fe	2.9	0.93	BCC, Im3m
Bi	4.5, 11.9	0.37, 0.05	hex-R, R3barm
Na	4.3	0.41	BCC, Im3m
Au	4.1	0.46	FCC, Fm3m
Mg	3.2	0.75	HCP, P63/mmc

Note that since typical electron energies in real solids are generally less than 10 eV, we're mostly interested in dimensionless energies less than, say, 25.

Next