= cosh(
x) [even]
Since our problem has a reflection symmetry we might as well construct solutions with that same symmetry. That way if we match our conditions at one singularity, those conditions will automatically be satisfied at the other boundary. For our bound state problem, we construct even and odd solutions that satisfy the free Schrödinger's equation:
= cosh(x) [even]
= sinh(x) [odd]
Of course, beyond x=a/2 we will want normalizable solutions:
= N exp(-x)
Wavefunction continuity at x=a/2 requires:
cosh(a/2) = N exp(-a/2) [even]
sinh(a/2) = N exp(-a/2) [odd]
Slope discontinuity at x=a/2 requires:
Even: where s = a/2
- N exp(-a/2) =
sinh(a/2) - 2 cosh(a/2)
- cosh(s) = sinh(s) - 2 cosh(s)
(2/-1) = tanh(s)
(a/s-1) = tanh(s)
a = s(tanh(s)+1)
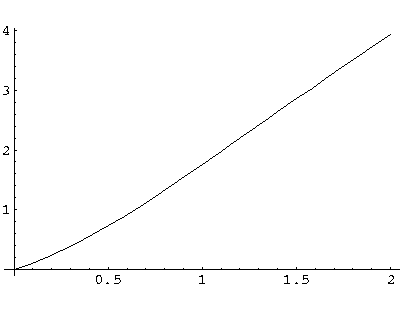
The function on the rhs (plotted above) is a monotonic function that ranges from 0 to 
.
It will equal any fixed value (like a) once. For small a, the intersection
will happen at small s..there tanh(s) ~ s<<1
so a = s, i.e., =2, E=-2. For large s
tanh(s) ~ 1, so a = 2s, i.e.,
=1, E=-½. Thus widely separated wells have the same energy as
a solitary well, and closely space wells have the same energy as one double-strength well.
Odd:
- N exp(-a/2) =
cosh(a/2) - 2 sinh(a/2)
- sinh(s) = cosh(s) - 2 sinh(s)
(2/-1) = coth(s)
(a/s-1) = coth(s)
a = s(coth(s)+1)
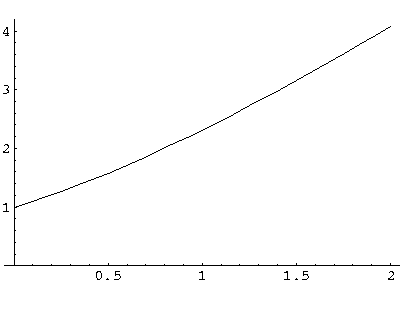
The function on the rhs (plotted above) is a monotonic function that ranges from 1 to .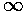
Thus it will equal any fixed value (like a) greater than 1 once.
For a=1, the intersection
will happen at small s=0, i.e., =0, E=0.
For large a he intersection happens at large s, there
coth(s) ~ 1
so a = 2s, i.e., =1, E=-½. Thus widely separated
wells have a nearly degenerate even & odd solutions. If the wells are brought closer the energy of
the odd solution increases to 0, and hence ceases to exist.
The below plot show the energy of these states a a function of 1/a. Thus the lhs corresponds to large separations, strong potentials, or little overlap between the solitary wavefunctions, whereas the rhs corresponds to small separations, weak potentials, strong overlap between solitary wavefunctions.
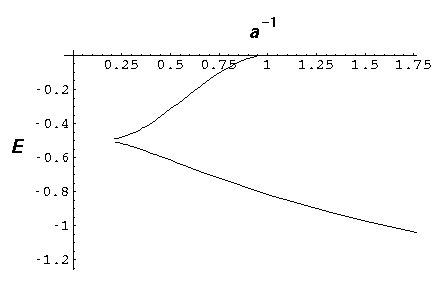
Notice that the odd wavefunction disappears at a=1. For small separations (rhs) the even solution reaches E=-2
Here are typical even and odd solutions (for a=4: a "large" separation).
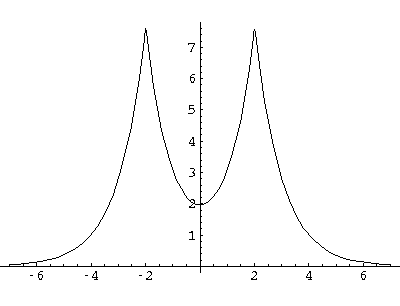
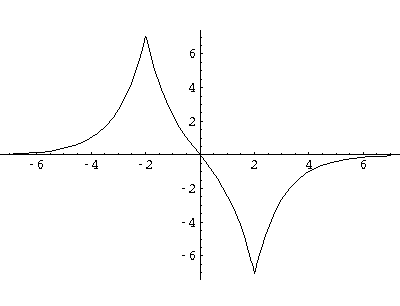
I would like this simple model to stand in for a complex problem: chemical bonding.
Consider that each delta functions represents the nucleus of a H-atom. We solve then
for the motion of one electron in this two-potential system: the ion H2+.
Notice that the ground state energy is consistently less for the combined system than
for the separated systems. If we add an additional energy, representing the
electrostatic nuclear repulsion: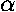 
/a, we form total energy plots
in which as a
0, the nuclear repulsion overcomes the
ever-smaller but finite electronic binding, to produce a minimum energy at some finite
separation:
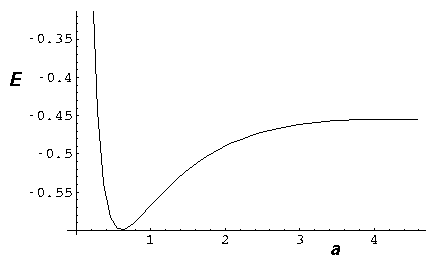
(The above calculation was based on 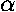=¼.)
Here you can see that the total energy is a minimum for a=.6.
In the Born-Oppenheimer approximation, we consider the motion
of the nuclei to be caused by a potential given by the total
(electronic + nuclear repulsion) energy as a function of a: E(a).
The essence of the approximation is that the electronic motion is fast compared
to the nuclear motion. The electron wavefunction continuously adjusts to the
changing nuclear separation. In this case we could imagine the nuclei executing
something like SHM around the energy minimum: a vibrating H2+ ion.
Note also that for separations greater than about 2, the energy is greater
than the isolated energy (-½), so some activation energy
is needed or else the nuclei cannot approach to the bonding distance.
The above calculation was based on the ground state wavefunction: the wavefunction whose eigenenergy decreased as the nuclei approached each other. Such a wavefunction would be said to be a bonding orbital The other wavefunction's eigenenergy increased as the nuclei approached; it would be called an anti-bonding orbital.
I should comment that the problem of an electron moving in the electrostatic
potential of two (separated) nuclei ("two-center problem") is exactly solvable,
but extremely complicated. We report below some simple results of this work. First,
the two-center problem (like the above two delta function problem) interpolates
between two easily solved problems: a pair of isolated atoms and a doubly strong united atom.
We can make a correlation diagram to show how the (symmetric [a.k.a. gerade: g]
and antisymmetric [a.k.a. ungerade: u]) linear combinations
of the isolated atom wavefunctions connect up to the doubly strong united atom
wavefunctions as a runs from
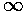to 0. Recall that the symbols 
,
, 
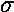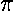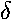, ... show that the angular momentum parallel
to the nuclear separation ("z axis") is 0,1,2,....
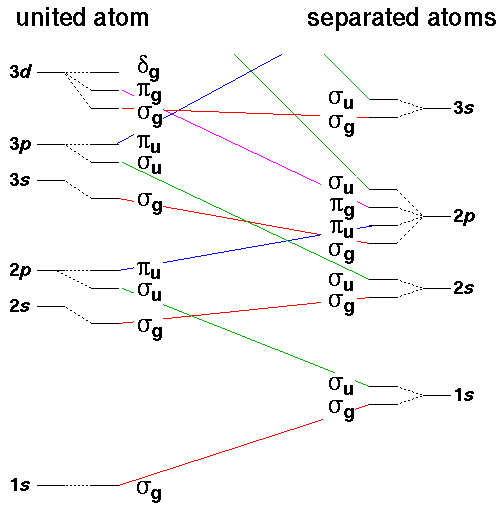
Note that even the anti-bonding ("u") levels remain bound (E<0) unlike our anti-bonding delta function wavefunction, which becomes unbound for separations closer than a=1.
Here is the electron energy for various separations:
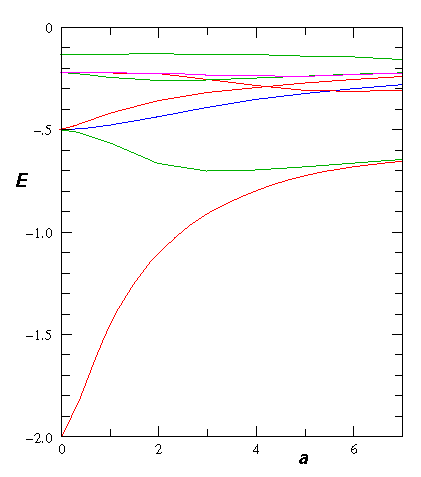
If we include the nuclear repulsion we find an energy minimum in the groundstate energy at about a=2 (we use here the dimensionless units for the H-atom: length in bohr radi, energy in hartrees). This there is a bound H2+ molecule.
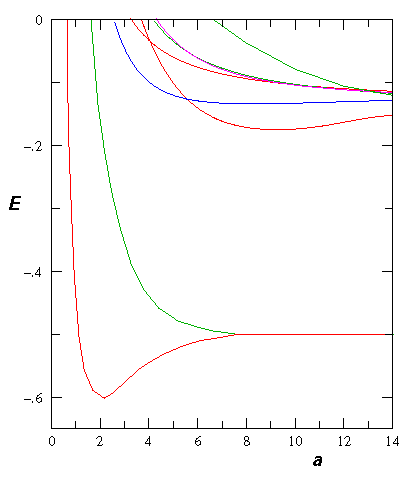
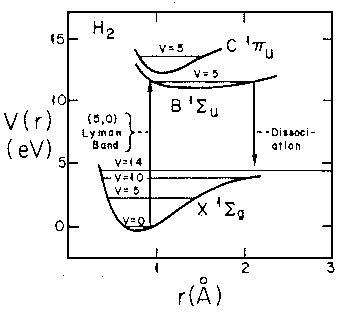
If we follow the aufbau principle, we should be able to put two electrons (spin paired: "singlet" state) in this state to produce a 2-electron molecule: H2. Of course, to do the calculation correctly we must include the electron-electron repulsion. In fact the stable equilibrium point moves in to about ¾Å (dimensionless: 1.5). Here is the energy level diagram for molecular H2. Note the vibrational levels marked in the diagram. Levels with vibration excitation v>14 lead to dissociation of the molecule.
