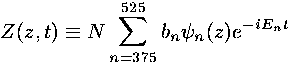
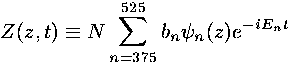
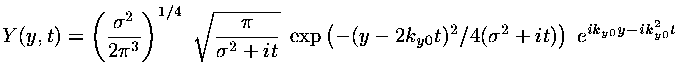
For this example I have chosen initial conditions:
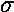 =5
=5
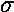 =5
=5
(Compared to previous examples, I have just expanded the y 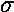 to match the z
to match the z 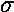 .)
The full wavefunction is just the product of these two factors:
.)
The full wavefunction is just the product of these two factors:
 (y,z,t) = Y(y,t) Z(z,t)
(y,z,t) = Y(y,t) Z(z,t)
and the probability density is  *
* .
.
Here are some pictures of the lump of probability as it begins its motion:
Here is a "multiple-time" image showing the probability density at t=0,3,6,9,12,15,18,21,24:
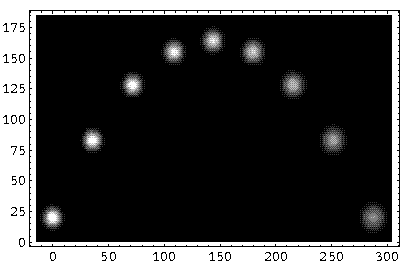
Notice the expansion of the wave-packet with time and the classical looking trajectory.
If one electron were fired with this wavefunction it would hit the "ground" at exactly one spot. If we fired electron after electron we would gradually build up the probable range of hit locations given by this wavefunction. Notice that much the same statement could be made of cannons whose projectiles follow Newton's laws. However we would attribute the variation in hit-location to variation in the initial velocity (say, due to variation in the amount of propellant or uncertainty in the angle of elevation) or variation in the forces active (say, due to varying wind conditions or atmospheric pressure). In QM we state that there is irreducible uncertainty even if the initial conditions and forces are identical in each shot. Thus there is not really a trajectory at all. The electron may be found here one time and there the following shot. All we have is a moving blob of probability density whose center may follow a path quite similar to the exacting trajectory given by Newton's laws. Finally I'd like to note that the above calculations, summing 150 Airy functions to find the probability density at a single point, are quite time consuming. It would be foolish to use this method of calculation on human-scale projectiles where macroscopic variations in conditions would swamp the irreducible uncertainty due to QM. Newtonian mechanics is a simple and accurate approximation of QM valid in most any human-scale problem.
The ballistic motion can be seen in greater detail by examining the following QuickTime movie (0.2 Mb) on a frame-by-frame basis.