SHM p.6
Seeing quantum mechanical oscillation
Classical mechanics (and most people above age 3)
have the notion of a particle's position. Quantum mechanics
says "particles" don't have positions, and says it applies to all
objects: big (where it replaces classical mechanics) and small
(where classical mechanics wasn't working too well).
Now unless we've all been living in
a dream world since age 3, QM must have something that corresponds
to our very real impression that objects have position. QM finds
that "normal" objects under "normal" conditions have a range of
possible positions that is so small, that for most purposes we
can take the center of the range of possible positions as
"the" position. For example if we wanted to localize a bacteria
cell (1 µm) to an accuracy of 1/10 its diameter,
the resulting uncertainty in speed would be: 10-12 m/s,
for a Bucky Ball (C60): .04 m/s, while for a helium atom:
800 m/s (which is comparable to its normal speed at room
temperature). Thus for most any object bigger than a small molecule,
the range of possible positions required by quantum mechanics,
is so small, that usually no harm results for just saying
that the particle is in the middle of the QM range. (This
statement is hedged because physicists work hard to make macroscopic
systems in which quantum mechanics is important; but these
rare beasts are rarely found outside of the lab.)
Now it turns out that if we use the information that the
particle is approximately at a particular location, we must
give up the idea that the particle has a definite energy.
The resulting probability density then does depend on time:
the middle of the probability density (which in the above
we connect with the idea of "a" position) is seen to move much
as classical mechanics says its mythical point particles
would move.
Let's start by seeing how this would all work classically:
we say the particle starts approximately at x0
but with some uncertainty: 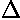 x0.
We release the particle on average with zero initial velocity,
but because of Heisenberg uncertainty relation, there must
be some spread of velocity
x0.
We release the particle on average with zero initial velocity,
but because of Heisenberg uncertainty relation, there must
be some spread of velocity 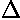 v0,
which is sometimes to the right and sometime to the left.
If we knew exactly
where the particle was starting from and its speed, we'd know
exactly where it was:
v0,
which is sometimes to the right and sometime to the left.
If we knew exactly
where the particle was starting from and its speed, we'd know
exactly where it was:
x(t)=x0cos(2t)+(v0/2)sin(2t)
(Why is  =2 in our dimensionless variables?)
=2 in our dimensionless variables?)
But because of the initial uncertainty in the velocity, there is varying
uncertainty in position:
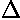 x(t)=
[(
x(t)=
[(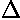 x0cos(2t))2+
(½
x0cos(2t))2+
(½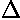 v0sin(2t))2]½
v0sin(2t))2]½
Thus the packet of probability expands and contracts as the central
value of the probability follows the usual classical relation:
x(t)=x0cos(2t)
Our particular application will have x0=10,
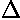 x0=0.31,
x0=0.31, 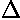 v0=3.8.
v0=3.8.
Here is the behavior of the classical probability distributions:
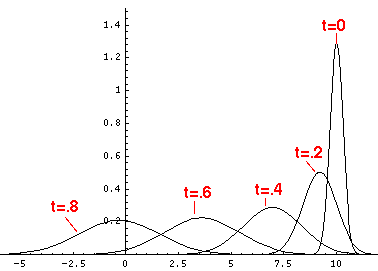
Here are the quantum mechanical results for t=0,.2,.4,...,1.6
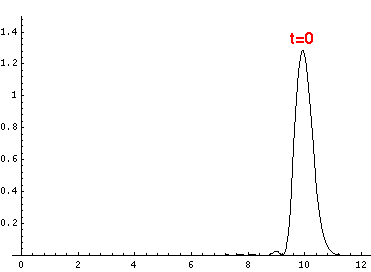
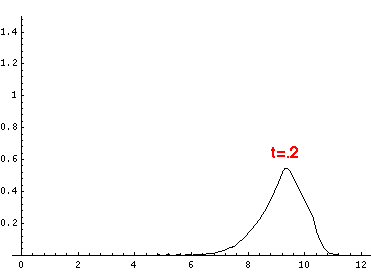
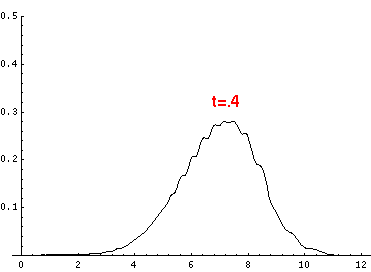
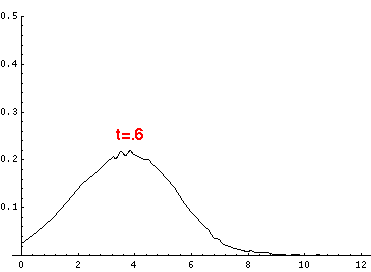
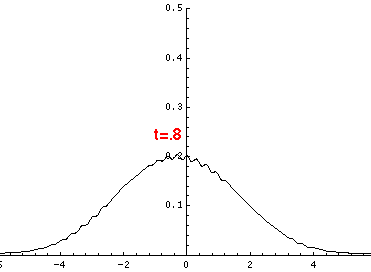
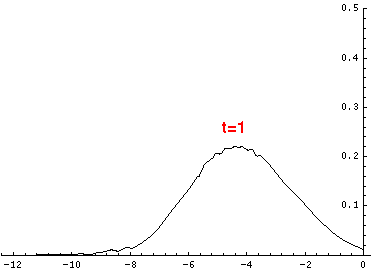
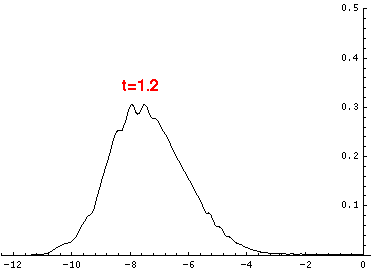
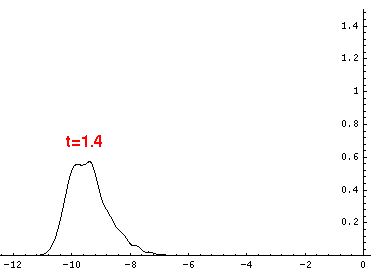
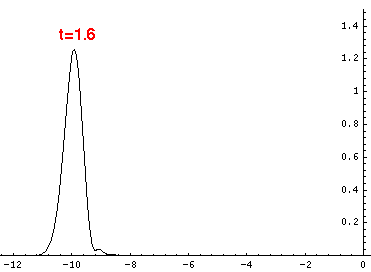
Here is the return motion.
Here is QuickTime movie showing these positions.
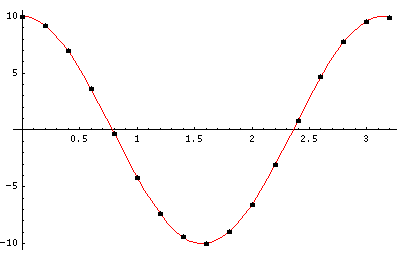
The last plot shows the average position of the wavefunction vs time. The red curve
is the classical result. Note that the "broadening" of the
wavefunction is simply the result of our uncertainty in the initial velocity.
Since the motion is exactly periodic, one period (T=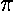 ) later the wavefunction
is exactly like that at t=0.
) later the wavefunction
is exactly like that at t=0.
Here is data on the location of the particle plotted above.
| t | x | | t | x
|
|---|
| 0 | 9.99 | | 1.8 | -8.97
|
| .2 | 9.20 | | 2.0 | -6.53
|
| .4 | 6.96 | | 2.2 | -3.08
|
| .6 | 3.64 | | 2.4 | 0.87
|
| .8 | -0.28 | | .6 | 4.69
|
| 1.0 | -4.17 | | .8 | 7.76
|
| 1.2 | -7.37 | | 3.0 | 9.59
|
| 1.4 | -9.42 | | 3.2 | 9.92
|
| 1.6 | -9.97 |
|
Next
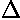 x0.
We release the particle on average with zero initial velocity,
but because of Heisenberg uncertainty relation, there must
be some spread of velocity
x0.
We release the particle on average with zero initial velocity,
but because of Heisenberg uncertainty relation, there must
be some spread of velocity 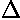 v0,
which is sometimes to the right and sometime to the left.
If we knew exactly
where the particle was starting from and its speed, we'd know
exactly where it was:
v0,
which is sometimes to the right and sometime to the left.
If we knew exactly
where the particle was starting from and its speed, we'd know
exactly where it was:
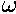 =2 in our dimensionless variables?)
=2 in our dimensionless variables?)











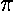 ) later the wavefunction
is exactly like that at t=0.
) later the wavefunction
is exactly like that at t=0.