SHM p.9

Oscillation in a Plane (2-d)

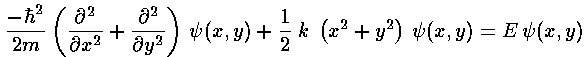
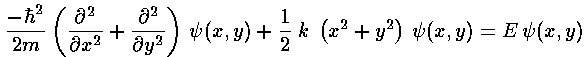
Proceeding exactly as before we have the dimensionless form

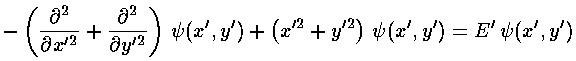
Since the total Hamiltonian can be written as the sum of Hamiltonians (one just in x' the other just in y', each exactly the same form as in the 1-d oscillator), the solution is just the product of 1-d oscillator wavefunctions (one just in x' the other just in y'):

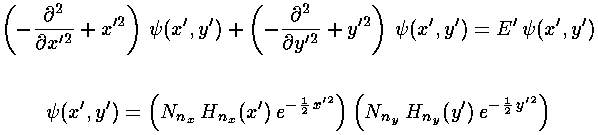
with E'= (2n_x+1 + 2n_y+1), i.e., the energy is just the sum of the "x" E' and the "y" E'. Note one new feature in the solution: there are different wavefunctions with the same energy (e.g., n_x=3 & n_y=0 ; n_x=2 & n_y=1 ; n_x=1 & n_y=2 ; n_x=0 & n_y=3 all have E'=8). This seemingly small difference turns out to be quite important; it's called degeneracy.

Here's what the probability density looks like for n_x=16 and n_y=4:

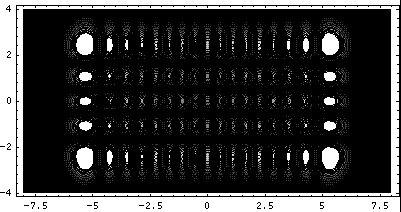
In this display the bright parts of the image are where the particle is likely to be found. Here is a expanded version of the same:

Note the 4 nodal lines perpendicular to y and the 16 nodal lines perpendicular to x.

Since the problem is rotationally symmetric rather than square-symmetric, it makes more sense to use a coordinate system that reflects the symmetry in the problem. Hence, I'd like to solve this problem is polar coordinates (r'-).

Changing coordinates changes the Schrödinger's equation to:

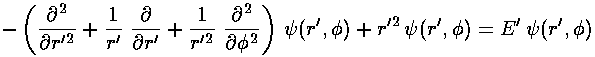
Seeking a solution where the dependence on r' factors from the dependence on ("separation of variables"), we find:

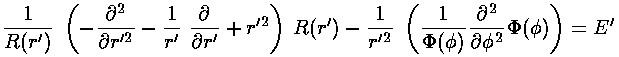
The solution to the 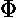equation is easy:

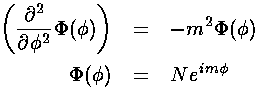
Our "boundary condition" is that if we go round the origin exactly once, the value of the wavefunction is exactly the same, i.e., the wavefunction must be the same at and +2: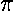

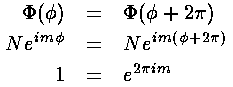
Hence m must be an integer.

This leaves us with the r' differential equation (given below in three equivalent forms):

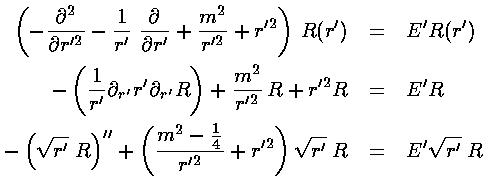
We have to work harder to solve this differential equation! Start by seeing how the the equation must work for large r'. The only term that has a chance of matching the ever growing r'² is the two-derivative term. Just as in the 1-d oscillator, an approximate cancellation requires exp(-½r'²) behavior.

For small r' only the derivative terms have a chance to match the ever growing m²/r'² term. If we try a power-law solution r'ⁿ

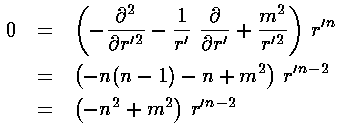
we find n=|m|.

Factoring out all the required behavior for large and small r', we hope to find a simple function (polynomial with luck) G(r') that contains the behavior for intermediate r'.

=r'^|m| exp(-½r'²) G(r')

So the next step is to rewrite Schrödinger's equation for G(r').

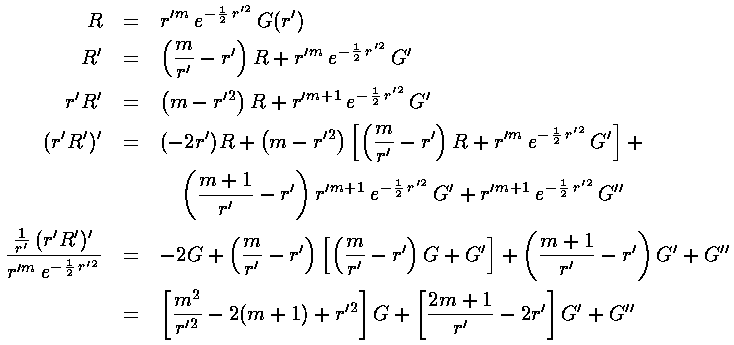
So:

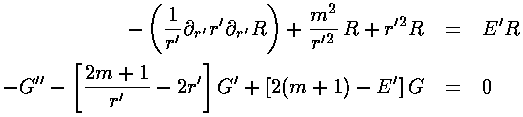
(In the above we've used m where we actually mean |m|.)

If we now try to write G as a polynomial:

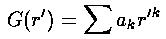
we can plug the polynomial form into the differential equation:

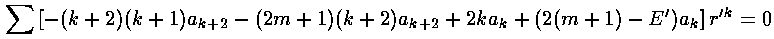
The result is a two term recursion relation (i.e., the result has just two as so, for example, given a₀ we can calculate a₂, from which we can calculate a₄, etc. until we're done.)

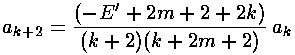
Note that the the recursion relation connects even k to even k. Since a₀ may not be zero (as if it were we'd factor out r', thus increasing the r'^m term to r'^m+1), the polynomials will have only even terms. Thus we write our even k=2i, where i is an integer.

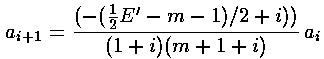
It turns out that the polynomial must end if the wavefunction is to be normalizable. One can show that the non-terminating sum gets at least as big as exp(+r'²), so instead of going to zero for large r' gets big like: exp(+r'²/2). The only way the sum can end is if the numerator of the recursion relation is zero, i.e., if

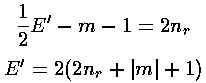
Thus if E'=2(2n_r+|m|+1) then a_i+1=0 for i=n_r (and hence all further as are zero) and the highest power of r'² in the polynomial is n_r.

Note that if we had tried for a polynomial solution for itself (rather than factoring out the r'^m exp(-r'²/2) first), we would get an (unsolvable) three term recursion relation.

The polynomials we have been calling G are Laguerre polynomials (see for example, Abramowitz & Stegun, §22 p. 771 or Szegö Ch.V).

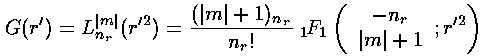
Here is the overall solution:

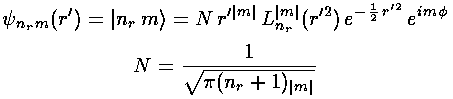
Here is what the probability density looks like for n_r=10, m=0 (again, the bright areas are places where the particle is likely to be found, the dark where it is unlikely to be found)

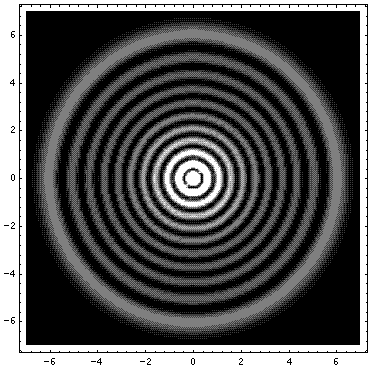
Note the solution is circle-symmetric and has 10 nodal circles.

Here is what the probability density looks like for n_r=5, m=10 (all of these density-plot solutions have E'=42)

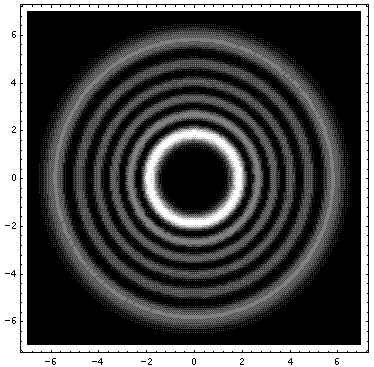
Note the solution is circle-symmetric and has 5 nodal circles, and that the particle is unlikely to be found exactly at the origin.

Note that in producing these circle-symmetric solutions, we have produced complex rather than real wavefunctions.... that factor of exp(im). This factor cancels out of our ^* probability density (so the probability density is circle-symmetric), but if we were to look at just the real part of we would find oscillation as a function of . Oscillation indicates momentum, so these solutions have angular momentum...in fact m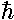 angular momentum in the "z" direction (i.e., perpendicular to the plane).

Because the angular dependence is "simple" we can usefully plot the wavefunction just as a function of r'. Here are "stacked wavefunction" plots for m=0,1,3:

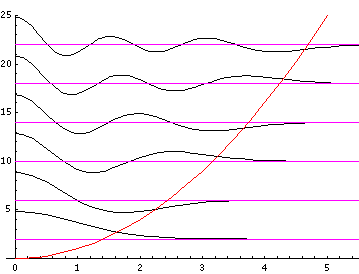
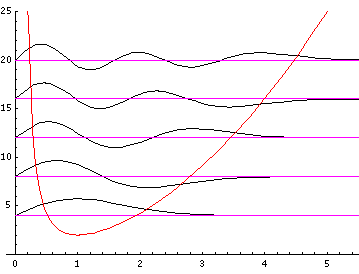
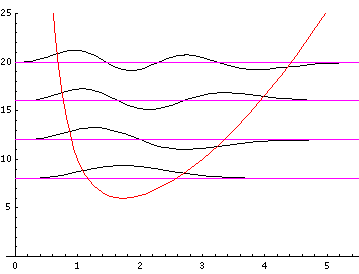
The red line is the classical "effective potential"= m²/r'²+r'² which includes the "centrifugal barrier" m²/r'² for a particle with z angular momentum m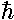. Because of the centrifugal barrier non-zero m wavefunctions are excluded from the origin.

Next