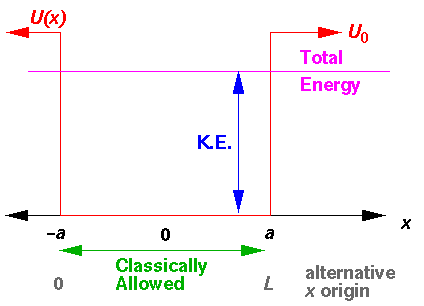

The above diagram plots various the energies involved as a function of position (x). The line representing "Total Energy" is flat, because total energy is conserved (i.e., is constant). Potential energy, U(x), is plotted in red: for |x|<a U(x)=0 and for |x|>a U(x)=U0. Total energy is the sum of kinetic energy and potential energy: thus kinetic energy is what you have to add to potential energy to get the constant total energy. Kinetic energy must be positive, so the only places the particle can actually go are where U(x)<E. The points on the edge of the allowed region (where U(x)=E, i.e., x=±a are called turning points. There the kinetic energy is zero, and so the velocity of the particle is zero. Just prior to reaching x=a, the particle is moving to the right (positive velocity). Just after reaching a the particle is moving to the left (negative velocity). At a the particle is momentarily at rest. The below plots the position and velocity as functions of time.
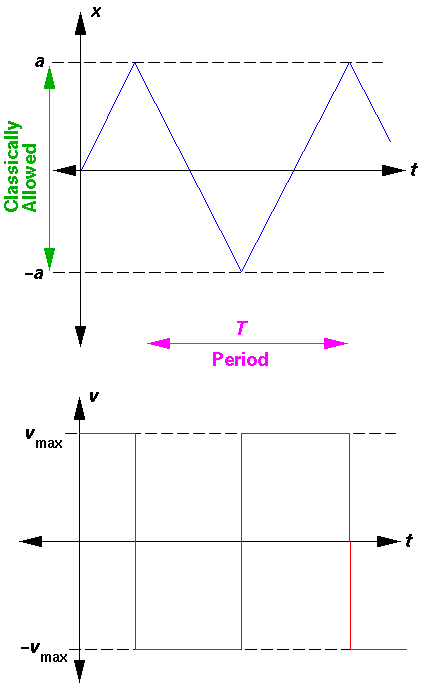
We will also find it useful to set up a square well with one edge at x=0 and the other at x=L (i.e., 2a=L). Clearly this shift in our choice of origin has no effect on the physics, but it occasionally will make the formulas a bit simpler.
It makes no difference to classical bound-state problems, but an even simpler version is the "infinite square well" in which the potential for |x|>a (U0) is taken to be infinite.
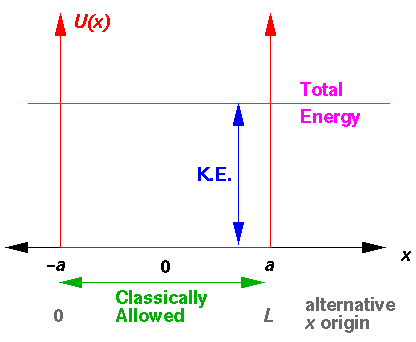
For the infinite square well, classically the particle is always confined to |x|<a, whereas for the finite square well, if the particles energy E exceeds U0 the particle will travel in the region |x|>a but at a reduced speed. In |x|<a the particle's speed is:
vmax=[2E/m]½
whereas in |x|>a it would be:
[2(E-U0)/m]½