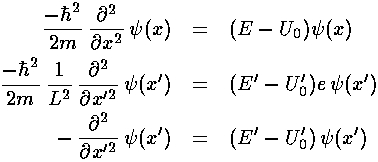
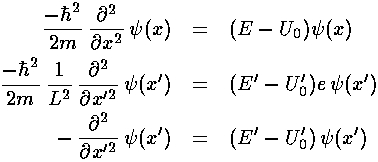
This last equation should remind you of the (Newtonian) differential equation
for a simple harmonic oscillator. (Note: derivatives with
respect to x rather than time and E'-U'0 rather than
 2.)
2.)
We consider now two cases: (1) where the energy is more than the potential energy (so there is real kinetic energy---the classically allowed region) and (2) where the energy is less than the potential energy (so there is negative (?!) kinetic energy---the classically disallowed region)
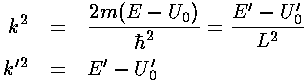
(It turns out the 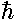 k is the particle's momentum.)
k is the particle's momentum.)
Substituting k into the differential equation gives:
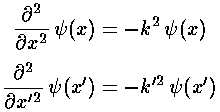
with well known solutions:
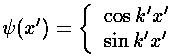
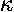 [Greek kappa] (we show
below both dimensionless and dimensioned versions):
[Greek kappa] (we show
below both dimensionless and dimensioned versions):
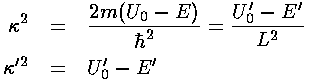
Substituting k into the differential equation gives:
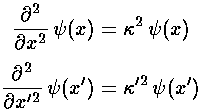
with well known solutions:
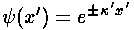
 (0)=
(0)=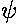 (L)=0
(L)=0
Since cos(0)=1, the cosine solution violates the boundary condition, and cannot be the
solution. sin(0)=0 automatically, but we must also have: sin(kL)=0
(or sin(k'1)=0). As is well known, sine has zeros at integer multiples
of 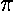 , so we must have:
, so we must have:
kL=n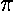
From which we find the energy:
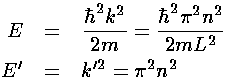
The normalized wavefunctions are:
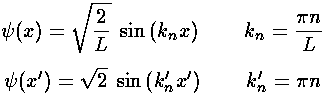
If we use the symmetric origin choice ("walls" at ±a) we have the same equations for the eigenenergies and k but the form of the trigonometric functions changes between even and odd n:
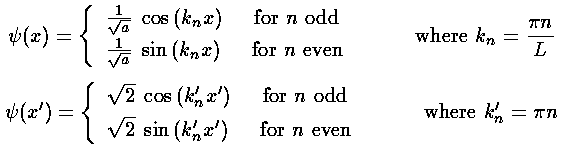
| n | E' |
|---|---|
| 1 | 9.87 |
| 2 | 39.48 |
| 3 | 88.83 |
| 4 | 157.91 |
| 5 | 246.74 |
| 6 | 355.31 |
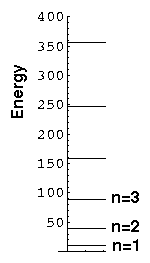
Notice that we have a discrete set of energy levels, i.e., energy is quantized and the particle can have only the above energies. Quantum mechanics says energies between these levels will not be seen in nature. A discrete set of levels is expected if the particle is confined to a region.
Notice that the energy levels become further apart as you go up in energy. (Energy spacing (i.e., differences) are quite important as (1) that is what is observed in emitted photon energies and (2) that is what is related to the classical period.)
In the quantum fall, energy spacing decreased with increasing energy. In the quantum oscillator, the energy spacing was uniform. Here the energy spacings increase with energy. In a homework problem, you are to show that in the WKB approximation the energy spacing is proportional to the classical frequency, i.e., inversely proportional to the period T. SO I claim that in the square well the period decreases with increasing energy, and in the quantum fall the period increases with increasing energy. Is this true?