
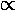 ± exp[-
± exp[- x]
x]

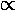 ± exp[-
± exp[- x]
x]
for x>a and

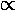 ± exp[+
± exp[+ x]
x]
for
x<-a as 
 0
as |x|
0
as |x|
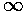 to produce
normalizable wavefunctions.
to produce
normalizable wavefunctions.
Our solutions for |x|<a are:
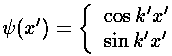
Inside the well the potential is zero so:
k'2=E'
For |x|>a we have:
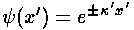
where:  '2=U0'-E'
'2=U0'-E'
Our matching points are x'=±½
(i.e., x=±a). The wavefunction and its derivative must
be continuous at the matching point. The second derivative of  will have a step at x=±a to match the step in potential as
required by Schrödinger's equation:
will have a step at x=±a to match the step in potential as
required by Schrödinger's equation:
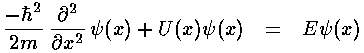
Thus we require:
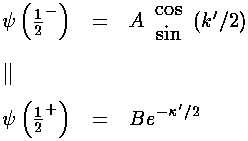
Here the expression 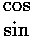 indicates that
we are to use the top item (cos) for odd n and the
bottom item (sin) for even n. The expression:
½- indicates evaluation a little less ("-") than ½
i.e., in the classically allowed region
and ½+ indicates evaluation a little more ("+") than ½,
i.e., in the classically disallowed region.
(Technically what's going on here is limits from the left hand side and
limits from the right hand side. We are making sure that our formulae
for
indicates that
we are to use the top item (cos) for odd n and the
bottom item (sin) for even n. The expression:
½- indicates evaluation a little less ("-") than ½
i.e., in the classically allowed region
and ½+ indicates evaluation a little more ("+") than ½,
i.e., in the classically disallowed region.
(Technically what's going on here is limits from the left hand side and
limits from the right hand side. We are making sure that our formulae
for  agree at the turning point.) A and B are unknown
constants having to do with the normalization of the wavefunction in each
region.
agree at the turning point.) A and B are unknown
constants having to do with the normalization of the wavefunction in each
region.
Now we match the derivative of  :
:
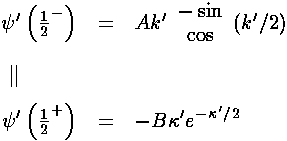
We can eliminate the unknowns A and B by dividing the second equation by the first.
For odd n we have:
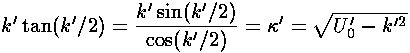
For even n we have:
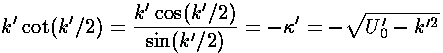
The quantity formed by dividing the derivative of  by
by  :
: 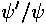 is known as the logarithmic
derivative since it is the derivative of ln(
is known as the logarithmic
derivative since it is the derivative of ln( ). Thus
we would say the above two expressions require the continuity of the
logarithmic derivative across the turning points.
). Thus
we would say the above two expressions require the continuity of the
logarithmic derivative across the turning points.
The above two equations are nonlinear equations we can solve
for k', and from k' we can find E'. The solutions,
of course, depend on U0'. Once we know k',
we can solve the  -match equations for A/B.
The overall scale of
-match equations for A/B.
The overall scale of  is set by the normalization
requirement:
is set by the normalization
requirement:
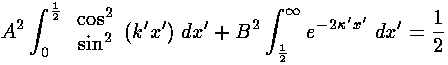
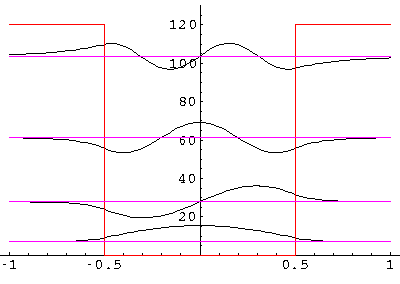
We are seeking the energy levels for various possible values of U0'. Here are the results for U0'=120:
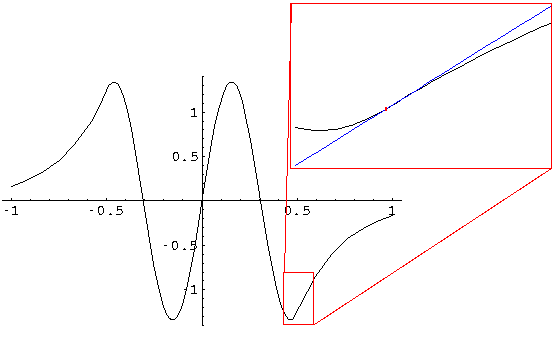
The match, so carefully made in the above work, is hard to
see. In the below we show the n=4 wavefunction and blow up
one matching region. Notice that on the left of x'=½
the curvature (second derivative) of  is positive
whereas on the right of x'=½ the curvature is smaller
and negative. The jump in curvature is required by Schrödinger's equation.
A line with the matching slope is shown in blue.
is positive
whereas on the right of x'=½ the curvature is smaller
and negative. The jump in curvature is required by Schrödinger's equation.
A line with the matching slope is shown in blue.
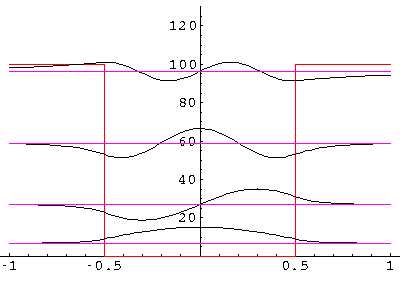
Here are the results for U0'=100:
If we reduce U0' to 80, the n=4 state is lost:
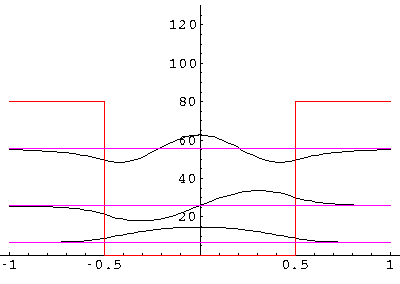
Notice that as U0' is reduced, all the states move
a bit lower in energy.
For example, the third state was at E'=61.3 for U0'=120
and moved to 55.6 for U0'=80. With U0'=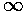 ,
third state has E'=(3
,
third state has E'=(3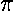 )2=88.8. Note how the probability of being found in
the classically disallowed region grows as E' nears
U0'. The smaller the energy "deficit"
in the classically disallowed region, the more likely it is
to find a particle in this "disallowed" region. As we said earlier, if U0'=
)2=88.8. Note how the probability of being found in
the classically disallowed region grows as E' nears
U0'. The smaller the energy "deficit"
in the classically disallowed region, the more likely it is
to find a particle in this "disallowed" region. As we said earlier, if U0'=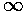 the wavefunction must be exactly zero in the disallowed region.
the wavefunction must be exactly zero in the disallowed region.
In the below plot we display the loss of states as U0' is reduced
from infinity (i.e., 1/U0' increases from 0). On the y-axis
k'/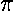 is plotted; Recall: E'=k'2.
For the infinite square well
k'=n
is plotted; Recall: E'=k'2.
For the infinite square well
k'=n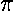 , so for 1/U0'=0 the nth
level's k'/
, so for 1/U0'=0 the nth
level's k'/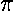 is n and and states exist for each whole number
n. As U0' is reduced each level's k' is reduced
until k'/
is n and and states exist for each whole number
n. As U0' is reduced each level's k' is reduced
until k'/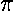 =n-1 at which point that level disappears.
Thus for U0'=100 (1/U0'=.01) we have but 4 levels left,
and the fourth is about to disappear.
=n-1 at which point that level disappears.
Thus for U0'=100 (1/U0'=.01) we have but 4 levels left,
and the fourth is about to disappear.
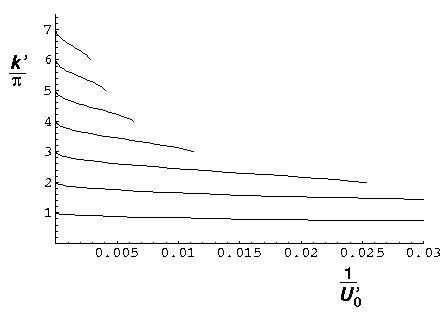
The n=2 level disappears at U0'=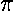 2
(near 1/U0'=0.1), the ground state remains for even
arbitrarily small U0'.
2
(near 1/U0'=0.1), the ground state remains for even
arbitrarily small U0'.