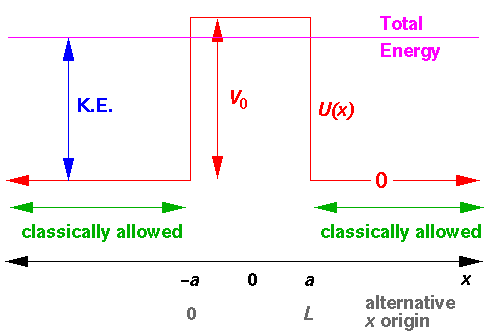
This is our new set-up for our square well:
I've drawn the above diagram with the additional "problem" that the energy is less than upward bump.
Classically if E>V0 the particle will be slowed as it enters the well, but the reflection probability is zero. Classically if E<V0 the bump is classically disallowed and the particle will always bounce off the well-wall; the reflection probability is 1.
In order to solve the problem quantum mechanically we need to do a bit more work than just let V0=-U0 in our previous solution because inside a classically disallowed bump the nature of the Schrödinger's equation solutions changes from sin and cos to sinh and cosh (i.e., we have exponential decay rather than oscillation in what has become a classically disallowed region). That is to say that
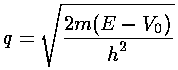
becomes complex when E<V0. Of course, as long as we remember
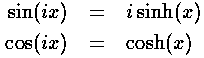
the transformation of sin to sinh will take place automatically as q becomes complex.
Here are plots of our reflection probability:
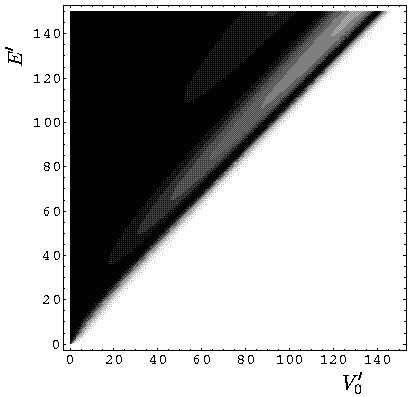
Notice that for E<V0 we have basically 100% reflection (more on the slight deviation later). For E>V0 we have oscillations that are identical in form to the oscillations on the previous page.
Here is a plot of the reflection probability as a function of E' for V0'=100:
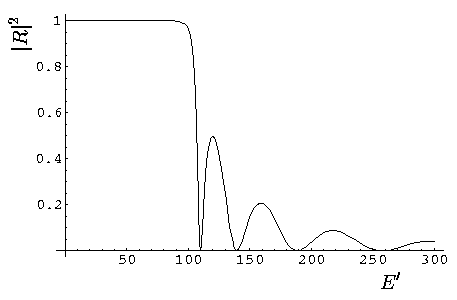
Careful examination of the previous plot shows that
as E'
100 the reflection
probability decreases from exactly one. Lets look at a plot of
the transmission near and below E'=100:
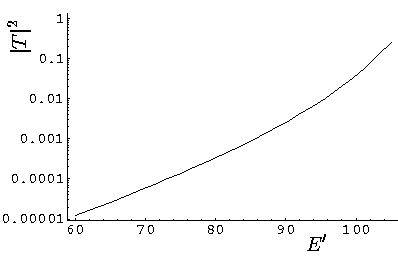
Note the exponentially small transmission becomes ever smaller as the region becomes more disallowed. These incredibly small "tunneling probabilities" are in fact of interest in nuclear physics. Most nuclei with atomic weight, A, more than about 140 (i.e., the bottom two rows of the periodic table) are energetically unstable to alpha decay. That is to say that the Z-2 A-4 nucleus plus alpha particle weighs less than the original nucleus. We can think of the alpha particle as being in a high energy wavefunction unable to escape over the nuclear barrier. Here is the picture:
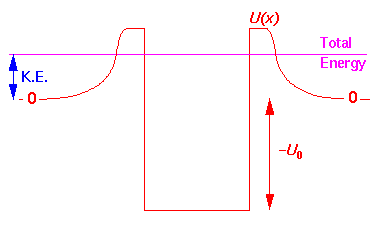
The idea is that the alpha is bouncing around inside the barrier (at quite high speed, with say 1020 bounces per second). While the alpha has the energy to escape, classically it cannot escape because of the barrier is a classically disallowed region. In quantum mechanics there is a small tunneling probability, so it can escape given enough time. If the alpha's energy approaches the barrier top, the tunneling probability grows quickly and the half-life for the decay shrinks correspondingly. Alpha decay half-lives span a remarkable range: form so short we can't measure it (10-9 sec) to so long we can't measure it (1016 year).
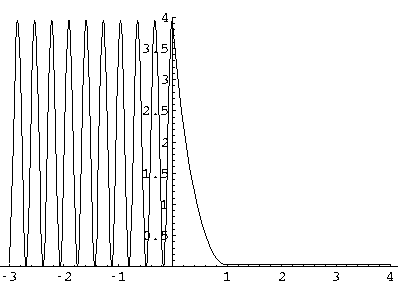
Since the wavefunctions are complex they are difficult to display as a x-y plot. We begin by displaying the real part of a slightly below barrier wavefunction (E'=99, V0'=100 with a transmission probability of about .03):
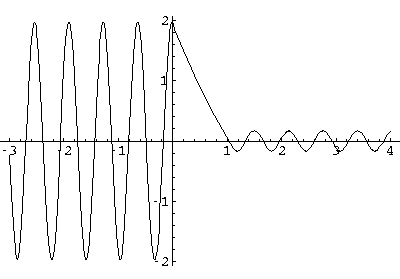
Note: the exponential decay inside the barrier, with a small amplitude, oscillatory wavefunction beyond the barrier. Here probability density plot for this wavefunction:
