Square Wells p.8

Round Square Wells

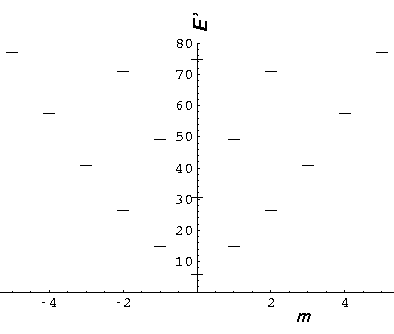
In polar coordinates Schrödinger's equation reads:

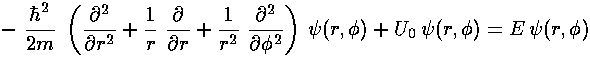
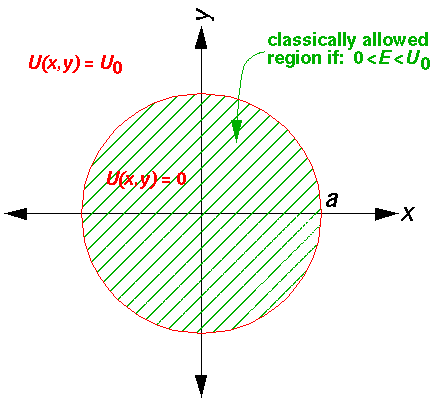
Inside the well, where the potential is zero, U₀ would be set to zero.

Taking a as our length scale and 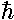²/(2ma²) as our energy scale, we gain the dimensionless form

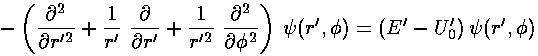
Seeking a solution where the dependence on r' factors from the dependence on ("separation of variables", =R(r')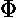()), we find:

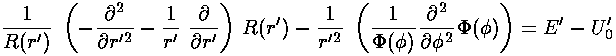
The solution to the 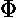equation is easy:

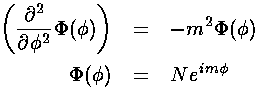
Our "boundary condition" is that if we go round the origin exactly once, the value of the wavefunction is exactly the same, i.e., the wavefunction must be the same at and +2: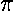

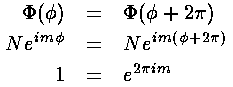
Hence m must be an integer. Since the radial equation only depends on m², the sign of m does not affect R, and we'll assume below that m is positive (i.e., in the below "m" is really |m|).

This leaves us with the r' differential equation. We will find it convenient to divide the above equation by E'-U₀', but we will need to pay attention as to the sign of (E'-U₀'). When (E'-U₀')>0 we are in a classically allowed region, and we expect the wavefunction to oscillate with a wavelength that depends on the particle's momentum... sin(kr) like solutions are to be expected. When (E'-U₀')<0 we are in a classically disallowed region, and we expect the wavefunction to exponentially decay...exp(-r) like solutions are to be expected. We'll handle both cases at the same time, sometimes by using ± signs where the top case (+ here) refers to a classically allowed region and the bottom case (- here) refers to a classically disallowed region. We substitute:

in our r' differential equation, producing a differential equation which I'll write in three equivalent forms:

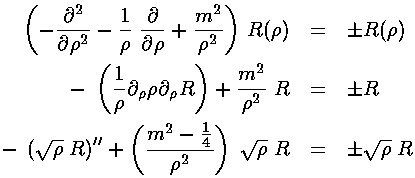
As usual we'll have to work to solve the radial differential equation! Start by seeing how the the equation must work for large 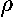. If in the last equation we ignore the (very small) 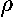^-2 term, we get the familiar oscillator differential equation. For E>U₀ we find:

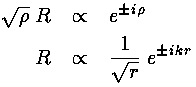
That is we see the expected oscillations as a function of r', but for large r' with ever smaller amplitude, because of the 1/r^½ factor.

For E<U₀ we find:

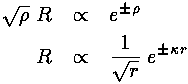
That is we see the exponential behavior as a function of r' expected in a classically disallowed region.

For small 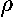, the 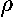^-2 term dominates and we can ignore the right hand side in comparison. If we try a power-law solutio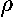n ⁿ

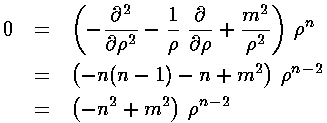
we find n=|m|.

Factoring out all the required behavior for small 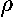, we hope to find a simple power series for R:

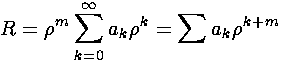
Plugging this in to the first R equation:

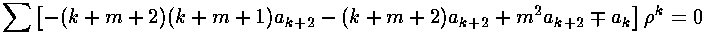
Or:

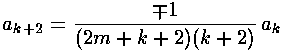
(In the above we've used m where we actually mean |m|.) The result is a two term recursion relation (i.e., the result has just two as so, for example, given a₀ we can calculate a₂, from which we can calculate a₄, etc. until we're done.) Note that the the recursion relation connects even k to even k and since a₀ may not be zero (as the leading term ^m was needed to make the small differential equation work). Thus the series will have only even terms and we write our even k=2i, where i is an integer.

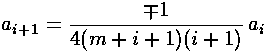
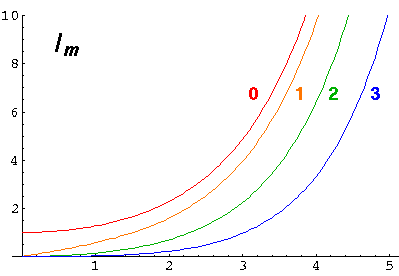
The series does not terminate; the result (for E>U₀) can be recognized as the Bessel function J_m from the hypergeometric formula (₀F₁).

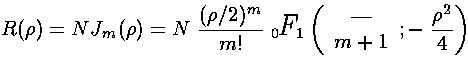
As we expect that a second order linear differential equation should have two independent solutions, we're only half way there. J_m is regular at =0, the other Bessel function: Y_m (also known as N_m) explodes at =0, and hence is not part of normalizable wavefunctions. Here are the basic large and small argument behaviors of J_m and Y_m.

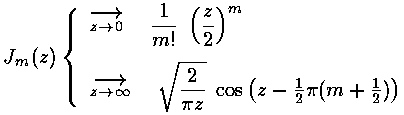
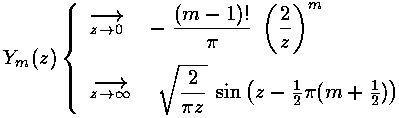
As we showed above, for large we expect oscillations like exp[±i].

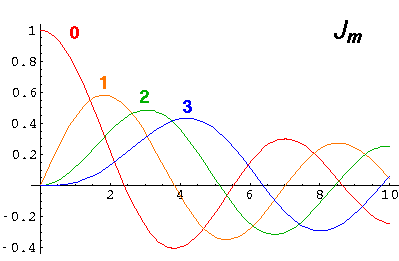
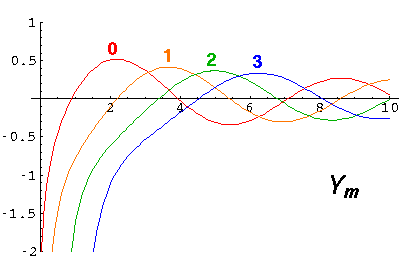
Y and J are real functions and hence oscillate like sin and cos. If we want, we can put Y and J together to produce something that for large oscillates like exp[±i]. The results are called Hankel functions:

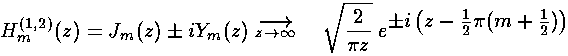
For E<U₀ we've found the exponentially rising modified Bessel function I_m:

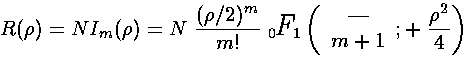
As above there is a second solution that is exponentially falling called K_m:

Infinite Round Square-Well

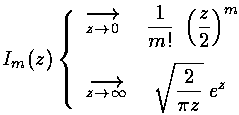
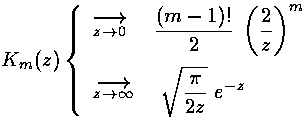
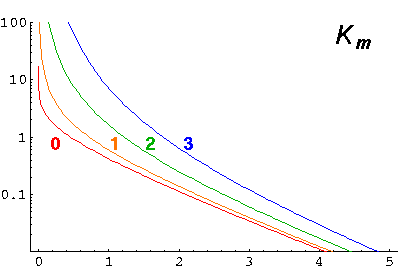
J_m(k'r')=0 for r'=1

That is k' must be a zero of J_m. The energy of the wavefunction can then be calculated from

E'=k'²

Here is the overall solution:

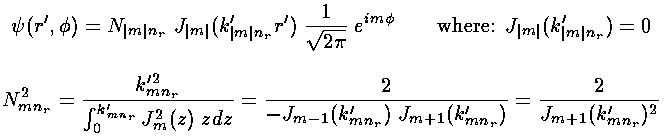
Here is what the probability density looks like for n_r=10, m=0 E'=1141 (again, the bright areas are places where the particle is likely to be found, the dark where it is unlikely to be found)

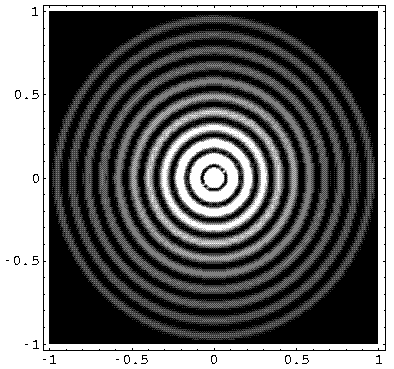
Note the solution is circle-symmetric and has 10 nodal circles.

Here is what the probability density looks like for n_r=5, m=10 E'=1038

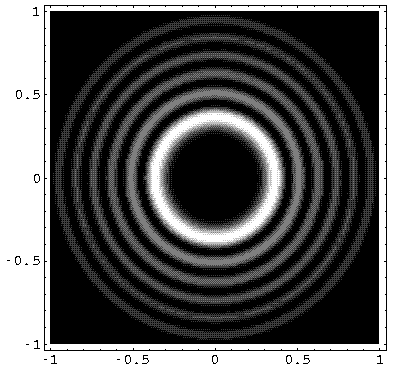
Note the solution is circle-symmetric and has 5 nodal circles, and that the particle is unlikely to be found exactly at the origin.

Of course the centrifugal potential is the source of the exclusion from the origin, but a more visual explanation comes from plotting the classical (no-force and hence straight line) trajectories of a particle with fixed angular momentum L'=10 and E'=1037.6:

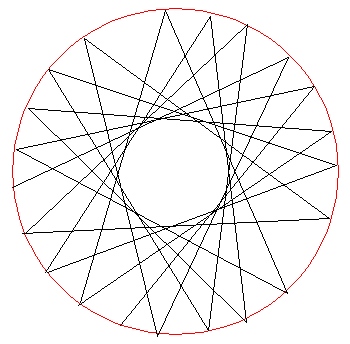
Note that in producing these circle-symmetric solutions, we have produced complex rather than real wavefunctions.... that factor of exp(im). This factor cancels out of our ^* probability density (so the probability density is circle-symmetric), but if we were to look at just the real part of we would find oscillation as a function of . Oscillation indicates momentum, so these solutions have angular momentum...in fact m angular momentum in the "z" direction (i.e., perpendicular to the plane).

Because the angular dependence is "simple" we can usefully plot the wavefunction just as a function of r'. Here are "stacked wavefunction" plots for m=0,1,2:

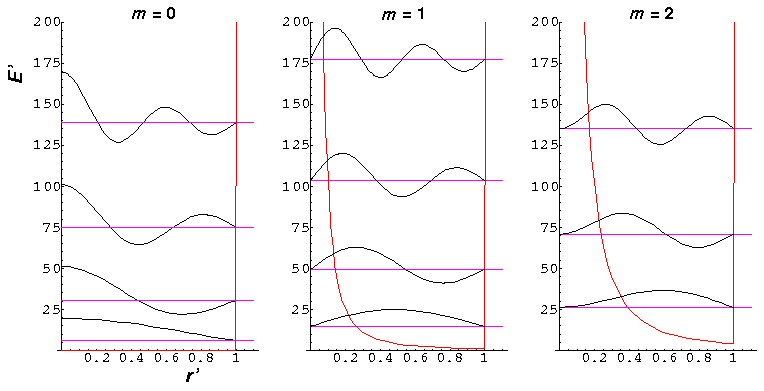
The red line is the classical "effective potential": m²/r'² (which is the "centrifugal potential") plus the infinite square well. Note that the centrifugal barrier excludes non-zero m wavefunctions from the origin.

m,nr	root	E'
0,0	2.4	5.78
1,0	3.8	14.68
2,0	5.1	26.37
0,1	5.5	30.47
3,0	6.4	40.71
1,1	7.0	49.22

You should check each of the above roots on the above plots of J_m.

Next