Square Wells p.10

Reflection from a Two Dimensional Step

We consider next the unbound 2-d step potential. We begin with a simple step potential: for x<0 U=0 and for x>0 U=-U₀. We employ the language of light reflecting/refracting off of a semi-infinite sheet of glass. (We avoid the very interesting physics of multiple reflection from a finite thickness of glass...an etalon.)

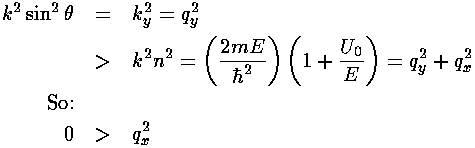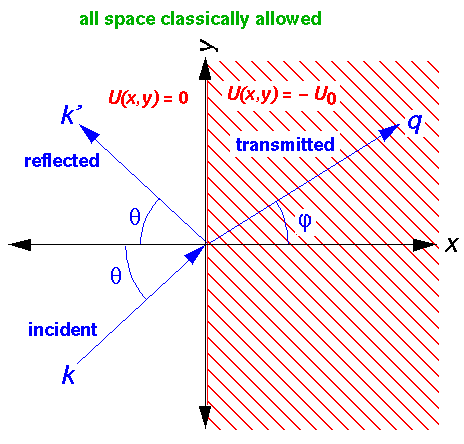
Classically, the downward step in potential at x=0 corresponds to an infinite force in the x direction located just on the x=0 line. Everywhere except x=0 the potential is flat, and so we are almost always in a no-force (i.e., "free particle") situation. Particles move with the speed required for their energy. On the left hand side:

p²=2mE

and on the right hand side we have a faster speed:

p²=2m(E+U₀)

Since there is no force in the y direction, the momentum in the y direction: p_y is conserved, even at the potential step. Thus when a particle makes the energy jump at x=0, p_x must increase to supply the increase in kinetic energy. Since p_x is enlarged and p_y is conserved, the direction of the particle changes. We find:

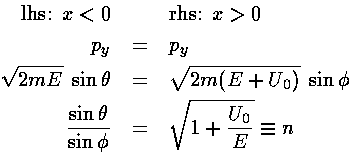
We see that the particle is Snell's Law "refracted" as if with an "index-of-refraction" n. Newton used such a particle-based explanation for the behavior of light. We note some oddities:

Moving into a more "optically dense" material (i.e., n>1, like from air to glass) the particle increases in speed. For light, we find the speed of light is slower in glass than in air.
The "index-of-refraction" n depends on the particle's energy: higher energy corresponds to smaller n. For visible light in most materials, higher energy means larger n
A step up in potential (e.g., U₀<0) corresponds to n<1. For light that would be like a transition from glass to air.
Classically we have no reflection. As I commented before, even in the WKB approximation there is no reflection; reflection is a result of a large change in potential in a wavelength or so of the wave.

Schrödinger's equation for our problem is:

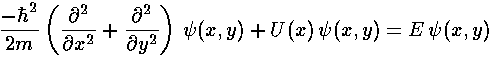
Thus:

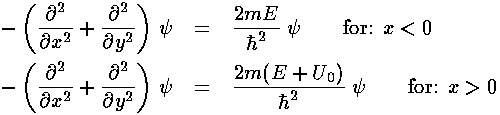
with solutions:

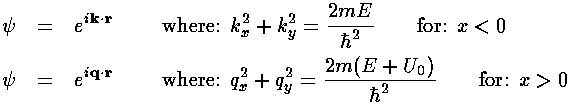
We note that Schrödinger's equation does not require, say, q_x, to be a real number, only that q_x²+q_y² have a given value. If q_x is imaginary, we can have exponentially decaying solutions like: exp(-|q_x|x).

Note that since we no longer have a finite sized box we've lost our length scale. We are forced to use dimensioned coordinates.

We now consider a solution that includes incident, reflected, and refracted waves:

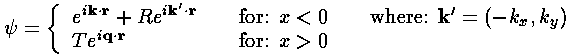
As usual we must match and 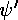along the boundary x=0. Thus we end up considering the values of 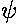for r=(0,y) and produce functions like:

exp(ik_yy) and exp(iq_yy)

If k_y does not equal q_y we would have different wavelengths on each side of the boundary so while we could match at a point, there would be no hope of matching all along the boundary. Thus we immediately produce the "refraction" condition that:

k_y=q_y

We now proceed to match 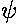and 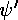and derive the reflected amplitude R:

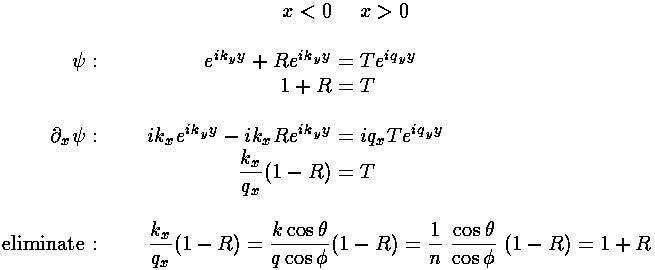
Since:

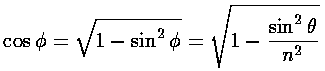
We can simplify our expressions for R:

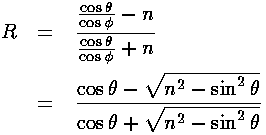
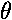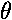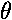We note that quantum mechanical reflection is exactly the same as the reflection of TE polarized light. Note the obvious check that here is no reflection if n=1. At normal incidence (=0) R=(1-n)/(1+n). At grazing incidence (=90°) R=-1. If n<1 (i.e., U₀<0) we can have total internal reflection for sin>n. As we show below, we have produced an imaginary q_x, so the "transmitted" wave does not propagate, rather it decays away for positive x: