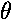 or
or 
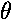 ),
angular speed (
),
angular speed (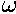 ), and angular acceleration
(
), and angular acceleration
(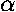 );
the equations relating these quantities are summarized in some texts on the
InfoMall.
);
the equations relating these quantities are summarized in some texts on the
InfoMall. Write your solutions to the following problems and submit them before 6 am on Monday, March 3rd.
Submit to the SUBMIT FOLDER on Priscilla or as an attachment to an e-mail message to rfuller@unlinfo.unl.edu or using the above WWW link.
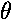 ,
, 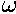 ,
, 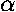
OBJECTIVES:
Keywords: rotational kinematics, angular displacement, angular velocity, angular acceleration, rotational equations of motion, rotational dynamics, moment of inertia
Commentary:
Rotational Motion--There is a motion of a system of masses that is as simple as the motion of a point mass on a straight line. It is the rotation of a rigid body about a fixed axis. For example, we live on a rotating earth, use rotating devices such as a potter's wheel or a phonograph turntable, and test our luck with a spinning roulette wheel. All of these are objects whose motion is described by the time dependence of a single variable, the angle of rotation. We shall study the angular equivalent of uniformly accelerated motion for some rotating objects.This lesson also begins the study of rotational dynamics by introducing the dynamic quantities torque and angular momentum for a point mass moving in a plane.
I. ROTATIONAL KINEMATICS
Keywords: Rotational Kinematics; Angular Displacement; Angular Velocity; Angular Acceleration; Rotational Equations Of Motion
OBJECTIVE:
PREREQUISITE:
Describing the motion of a body in uniform circular motion
Commentary
In this lesson, we recognize that a body rotating with respect to some axis
can also experience an angular acceleration, i.e., it can rotate faster or
slower. Rotational motion can be described in terms of a set of variables, and
relationships among them, that are quite analogous to the variables and
relationships that describe linear motion. The rotational variables are angular
position or displacement (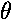 or
or 
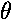 ),
angular speed (
),
angular speed (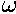 ), and angular acceleration
(
), and angular acceleration
(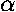 );
the equations relating these quantities are summarized in some texts on the
InfoMall.
);
the equations relating these quantities are summarized in some texts on the
InfoMall.
In keeping with trigonometric convention, we take to be increasing positively in the counterclockwise direction. Note that although angular displacements are "dimensionless," they are not unitless: consistency in the units used for angular measure (radians, degrees, or revolutions) is just as important in solving a problem as consistency of any other units.
II. ANGULAR-LINEAR KINEMATIC RELATIONS
Keywords: Rotational Equations Of Motion Rotational Kinematics; Kinematics; Fundamental Motion; Learning Objectives
OBJECTIVE:
The following figure illustrates the basis for a useful set of relationships between angular and linear descriptions of circular motion:
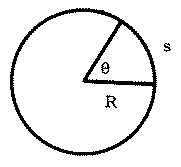
if
the angle 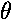 is measured in radians, then the arc length
is measured in radians, then the arc length
s = R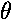 .
.
For a body rotating about a fixed axis, each point in the body moves in a circle concentric with the axis of rotation. The radius R of the circle is the perpendicular distance of the point from the axis.
Using the definitions developed in the preceding section for angular kinematic variables and the definitions for the magnitudes of the linear kinematic variables, we obtain the following relationships:
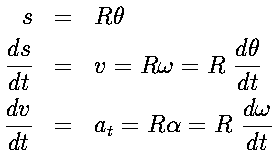 .
.
where s, v, and at are tangential
linear distance, speed,
and acceleration, respectively; and  ,
, 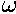 and
and
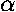 are the corresponding angular quantities.
are the corresponding angular quantities.
The above relationships of allow you to construct a table of corresponding linear and angular equations for circular motion with constant acceleration.
III. MOMENT OF INERTIA
Keywords: Moment Of Inertia
OBJECTIVES:
COMMENTS:
In the discussion of rotational inertia the terms "rotational inertia" and "moment of inertia" may be used interchangeably.
The equation for the moment of inertia has both a summation form applicable to systems of discrete particles:
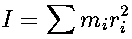 .
.
and an integral form applicable to continuous mass distributions:
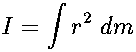 .
.
where r in either equation is the perpendicular distance of a mass element from the axis of rotation.
Note also that if one or more point masses are attached to any extended body, the rotational inertia of the resulting mass distribution is simply the sum of the rotational inertia of the extended body and that of the point mass(es) with respect to the same axis.
Calculating the moment of inertia for an irregularly-shaped mass can be a complex task, but the presence of the factor r2 in the expression for the moment of inertia should enable you to qualitatively compare the rotational inertias of equal masses that are distributed differently about their respective axes of rotation.
Other things being equal, the more mass a body has "away from the axis," the greater its moment of inertia will be.