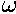= 0
in the inertial frame under consideration.Your responses to the Physics InfoMall search questions are due before 6 am on Monday, March 10th.
You may submit your answers to the SUBMIT FOLDER on Priscilla or as an attachment to an e-mail message to rfuller@unlinfo.unl.edu or using the above WWW link.
Using the keywords and the InfoMall to find explanations appropriate to your understanding of the physics of:
Equilibrium of Rigid Bodies
Write your solutions to the following problems and submit them before 6 am on Monday, March 10th.
Submit to the SUBMIT FOLDER on Priscilla or as an attachment to an e-mail message to rfuller@unlinfo.unl.edu or using the above WWW link.
Commentary:
Most of the objects that one sees are in a state of equilibrium, that is, at rest or in a state of uniform motion. Many man-made structures are designed to achieve and sustain a state of equilibrium, and this, in turn, sets requirements for the structural components (such as their sizes and shapes) that can be used. This lesson will give you some practice in analyzing the forces that result in equilibrium. From this analysis, if you are given the values of an appropriate set of forces you can find the remaining ones. On the other hand, in designing a stable system you can find the requirements for materials and dimensions that will ensure equilibrium.
OBJECTIVE:
Commentary:
The conditions acm = 0 and a = 0 can
describe a system that is in
either static equilibrium or dynamic equilibrium; for simplicity, we will focus
primarily on cases of static equilibrium, that is, on systems for which
vcm = 0 and 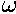= 0
in the inertial frame under consideration.
The first condition of equilibrium, that the net external forces on the body must be zero, alone is sufficient to establish equilibrium for a particle (point mass); by definition, a particle has no extent in space, so that all forces acting on it must act at a point and therefore the torque about any axis through the particle is zero. We made use of this simplification in our study of Newton's laws when we used vector addition to determine the single force that would balance a set of forces acting on a particle. In effect, a particle has only three degrees of freedom corresponding to translation along the three coordinate axes. The first condition of equilibrium is generally not sufficient to determine the equilibrium of an extended rigid body, since forces may act at different points on the body and thus exert a net torque on it even though they add vectorially to zero. This gives rise to the second condition of equilibrium for a rigid body: that the net external torques on the body must be zero.
The two conditions of equilibrium give rise to six separate equations, all of which must be satisfied simultaneously. This is not a trivial problem in the general case, but fortunately it is often possible to simplify the solution since many problems involve coplanar forces; in such cases, one force-component equation and two torque-component equations are automatically satisfied if the coordinate system is properly chosen.
Virtually all manmade structures designed to achieve static equilibrium exist in a uniform gravitational field. Applying the equilibrium conditions to a rigid body in a gravitational field would be an exceedingly complex task were it not for the fact that all of the gravitational force components acting on the uncountable mass elements that make up the body are equivalent to a single force applied at its center of mass. This single force, acting at the center of mass, can also be used to calculate the gravitational torque on the body about any point.
Commentary:
The solutions to the problems in this lesson are rather formal; that is, all problem solutions follow a regular procedure, which, if done carefully, will almost always produce the desired result. After learning the general procedures and practicing on a few examples, you should find no difficulty in solving any problem in this lesson.
The steps in the formal solution procedure are summarized here: