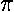2 = 10
Your responses to the Physics InfoMall search questions are due before 6 am on Monday, March 17th.
You may submit your answers to the SUBMIT FOLDER on Priscilla or as an attachment to an e-mail message to rfuller@unlinfo.unl.edu or using the above WWW link.
Using compound search and the InfoMall to find explanations appropriate to your understanding of the physics of:
Law of Grav*
Write your solutions to the following problems and submit them before 6 am on Monday, March 17th.
Submit to the SUBMIT FOLDER on Priscilla or as an attachment to an e-mail message to rfuller@unlinfo.unl.edu or using the above WWW link.
OBJECTIVE:
The members of the solar system - the sun, the moon, and the planets - have held a strong fascination for mankind since prehistoric times. The motions of these heavenly bodies were thought to have important specific influences on people's lives--a belief that is reflected even today in horoscopes and astrological publications. A revolution in man's thinking that occurred about four hundred years ago established the concept of a solar system with planets orbiting about the sun and moons orbiting about some of the planets. Copernicus, Kepler, Galileo, and Newton were the four scientific leaders chiefly responsible for establishing this new viewpoint. One of its very practical aspects, yet difficult for us earth-bound creatures to grasp, is that the force of gravity gradually diminishes as one recedes from the earth, in a way beautifully stated by Newton in his universal law of gravitation. Gravity is a universal force: it acts on every material thing from the smallest nuclear particle to the largest galaxy. It even acts on objects that have zero rest mass, such as photons--the fantastically minute "chunks" in which light comes. One of the most exciting areas of astronomical research today is the "black hole," where the gravitational field may be so intense that not even light can escape! Newton's law of gravitation is important not only in itself, but also because it serves as a model for the interaction of electric charges, which you will study later. Not only are the force laws and the potential-energy functions nearly the same, but the concept of a field carries over and becomes even more useful in the calculation of forces between electrically charged particles.
Commentary
The law of universal gravitation, as originally formulated by Newton, is summarized in the following statement: the gravitational attraction between any two particles is directly proportional to the product of their masses and inversely proportional to the distance between them. This law is expressed in symbolic form by
F = GM1M2/r2
where M1 and M2 are the masses of the particles, r is their separation, and G is the universal constant of proportionality.
Experimental methods for accurately measuring the value of G were not developed until long after Newton's death; even today, its value is known less precisely than the values of many other fundamental constants. For our purposes, though, the value:
G = 6.67 × 10-11 N m2/kg2
will be entirely adequate.
The law of universal gravitation further specifies that the direction of F is exactly along the line joining the two masses under consideration.
We don't need M2 at all in thinking about the quantity g(r), which is called the gravitational field intensity or, more simply, just the gravitational field due to M1. This abstraction g associated with a single mass M1 occupies all space surrounding M1 whether other masses are present or not; at each point, it can be represented by a vector with the magnitude
|g| = GM1/r2
pointing toward M1. Physically, the gravitational field intensity at a given point is simply the acceleration a small (negligible mass relative to M1) object would experience if it were placed at that point.
The use of the concept of a force field to describe an interaction at a distance is an exceedingly important technique, and will be developed further in later lessons on electric and magnetic interactions. The gravitational field is a central conservative field; central because it acts along the line joining the interacting particles, and conservative (for energy) because it is possible to define a potential energy function of distance. From your study of torque and angular momentum, you will recognize that a particle subject only to the centrally directed gravitational force of another body experiences no torque; thus its angular momentum is constant, or "conserved." (For circular orbits, this reduces to the simple result that the speed is constant.)
Furthermore, as the particle changes its position in any kind of orbit, all decreases in kinetic energy are accompanied by equal increases in gravitational potential energy, and vice versa, so that the total energy remains constant. (Later in this lesson, you will make extensive use of the conservation of energy).
Numerical Values of various constants for use in gravitational problems:
G = (2/3) × 10-10 N m2/kg2
Mass of Sun = 2.0 × 1030 kg
Mass of Earth = 6.0 × 1024 kg
Mass of Moon = (3/4) × 1023 kg
Mass of Mars = (6.3) × 1023 kg
Earth to Moon distance = (3/8) × 109 m
g at surface of Earth = 10 m/s2
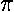2 = 10
Radius of Sun = 7.0 × 108 m
Radius of Earth = 6.4 × 106 m
Radius of Moon = (1/6) × 107 m
Radius of Mars = (1/3) × 107 m
Earth to Sun distance = 1.5 × 1011 m
Saturn to Sun distance = 1.5 × 1012 m
Problems Done in Class:
OBJECTIVE:
Commentary
If we use the customary symbol U(r) to denote gravitational potential energy, and equate this with the work done in moving a body from infinity to a radius r, the potential energy is just:
U(r) = -GMm/r
for a point or spherically symmetric mass.
A particle in such a gravitational field (with no other forces present) always moves in such a way that the sum of its kinetic and gravitational potential energies is constant:
Ei = Total initial (mechanical) energy
= Ki + Ui
= Kf + Uf
= Ef = Total final (mechanical) energy .
This energy-conservation equation is very useful in solving many problems.
Problems Done in Class:
OBJECTIVE:
Commentary
In reality, the orbits of planets and satellites are never exactly circles, but, rather, more general ellipses. However, the orbits of most planets and of many satellites are near enough to circular that only a very small error results from treating them as circular.
In fact, the centripetal force:
Fc = m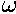
2r =
mv2/r
is required to hold a particle in a circular path.
In the case of a satellite moving around the Earth as in the figure below, this centripetal force is provided by the gravitational force of attraction between the Earth and the satellite.
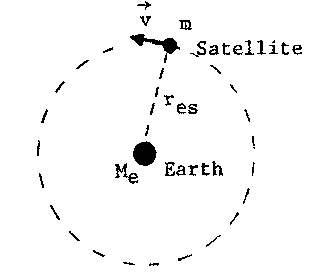
We can ignore the motion of the Earth, since with ME >> m the Earth acts like a fixed force center. Then, since the gravitational force acting on the satellite has the magnitude:
Fg = GMEm/rEs2,
we may equate Fc with Fg to obtain:
mv2/rEs = GMEm/rEs2
v2 = GME/rEs.
This relation allows us to calculate, say, v in terms of ME and
rEs. Once we have found v from a relation such as the above, then it
is a simple matter to find the period T of the circular motion, since vT is
just the circumference 2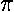r of the circular orbit. Similarly, we may begin with
information concerning the angular velocity of a satellite and calculate its
orbital radius.
Many communications satellites are placed in synchronous orbits around the Earth (a synchronous orbit is an orbit in which the satellite is constantly above the same spot on the earth's surface). How far above the surface of the Earth must such a satellite be?