T's positive,
that is, T(higher) -
T(lower). The results are the same--only the "bookkeeping" method is
different--but it is more customary to define a change in some quantity as the
final value minus the initial value.
Supplement:
How can we keep track of energy as it is transferred from one system to another? How can we calculate the amount of internal energy--a quantity that seems to be hidden within the very "guts" of matter? Further, what is the difference between temperature and heat, and between heat and work? This lesson focuses on the first of two central thermodynamic principles: the conservation of energy, or, as it is sometimes called, the first law of thermodynamics. The second basic principle, which deals with the inevitable increase of a quantity called entropy. These two abstract principles, plus a few other concepts and laws and the vocabulary needed for literacy in the field, are the entire content of thermodynamics. The energy and entropy principles form the framework that governs all energy conversions involving heat; they are the touchstones we must rely on as we attempt to create new energy devices, such as solar converters or fusion reactors, to limit the wasteful exploitation of the earth's resources. The approach of this module is macroscopic; that is, we shall deal with systems that are approximately of human scale in size and mass (thermometers, blocks of ice, heat engines), and we shall choose observable quantities such as pressure, volume, and temperature to describe the behavior of these systems. The macroscopic approach should be seen as supplementary to the microscopic approach, which regards the behavior of the atoms and molecules as fundamental. This latter framework chooses the molecular velocities, energies, and momenta as the starting point, and values for macroscopic observables are derived from the microscopic picture. The microscopic approach is treated in the next module where the behavior of gases is interpreted kinetically, that is, in terms of molecular energies and collisions.
I. TEMPERATURE AND THE ZEROTH LAW
Keywords: The Zeroth Law Of Thermodynamics; The Laws Of Thermodynamics; Systems; Learning Objectives
OBJECTIVES:
PREREQUISITE:
Recognizing methods and units used for measuring pressure
Supplement:
The concept of temperature is so ingrained in our everyday sensory experience that you may wonder why we present such a detailed discussion of the temperature scale and how temperatures are measured. It will be well worth your time, however, to find these discussions and to make sure that you fully understand how the Kelvin scale is derived. Thermodynamic temperature (in kelvins) is one of the seven fundamental quantities on which the International System of Units is based, and it is the key observable property tying together the macroscopic and microscopic approaches to thermodynamics. Since the temperature of 0 K (absolute zero) is inaccessible as a practical reference point, the international scientific community has agreed on a reference temperature that is readily reproducible as well as unique--the so-called triple point of water (specifically, of highly purified water that contains the same mixture of isotopes of hydrogen and oxygen that is found in sea water). By definition, the triple point of water is 273.16 K, or about 0.01 K above the more familiar "freezing" point (ice point). We use the subscript "tr" to denote measurements made at the triple point of water. The zeroth law of thermodynamics does not contain the word "temperature," but the concept of temperature is implicit in the phrase "thermal equilibrium". Given our definition of temperature in terms of a chosen thermometric property (such as gas pressure) we can say that two bodies are in thermal equilibrium if they are at the same temperature, and vice versa. We have not fully resolved the question of what it means for a thermometer, or any other object, to reach thermal equilibrium with some second object. For our present purposes, however, the definition of thermal equilibrium provided in this course will be adequate if we assume that two bodies are thermally "connected" (and will eventually reach equilibrium) if they are separated only by a thin layer of some noninsulating material such as metal.
EXAMPLE:
Suppose that you wish to identify an unknown liquid by measuring its boiling point accurately. The only instrument available is an uncalibrated constant-volume gas thermometer in which you measure the pressure (p) of the confined gas to be 2.6 x 104 Pa at the triple point of water. Then you bring the same confined gas to equilibrium with the unknown boiling liquid and measure p = 3.5 x 104 Pa.
Solution:
(a) Using the relationship between pressure and temperature of a low pressure gas thermometer, and recalling that the temperature of the triple point of water is defined to be 273.16 K, we have:
T(K) / 273.16 K = (3.5 x 104 Pa) / (2.6 x 104 Pa) ;
T = (3.5/2.6)(273.16) = 368 K ~ 370 K.
(b) T(°C) = T(K) - 273.15° = 95°C.
(c) Since water has a boiling temperature at standard pressure of 100°C, the liquid is probably water. (If the atmospheric pressure were below standard pressure during the experiment, it would explain the observed reduction of the boiling temperature.)
Practice Exercises:
II. HEAT, HEAT CAPACITY, AND LATENT HEAT
Keywords: Heat; Calorimetry; Heat Capacity; Latent Heats; Specific Heat;
OBJECTIVES:
Supplement:
The concepts of thermal equilibrium and thermal contact become more meaningful when we can interpret them within the context of heat transfer and heat capacity. We see that the thermal equilibrium of two systems is achieved through the transfer of heat and that two systems initially at different temperatures that are in thermal contact (i.e., arranged so that heat can be transferred between them) will reach a final (equilibrium) temperature that lies between the initial temperatures. In a "mixing" situation of this sort where no other interactions occur, the equilibrium temperature is determined solely by the initial temperatures and relative heat capacities of the systems in contact. Make sure that you understand the difference between heat capacity, which depends on the quantity of material, and specific heat, which is a property of the material itself (measured under prescribed conditions, e.g., constant pressure or constant volume). Some authors use the term "specific heat capacity," but this is synonymous with specific heat as used here. (Generally speaking, any physical quantity that is "specific" is defined in such a way that it does not depend on the size of the system under consideration.) The symbol Q is widely used to represent a quantity of heat, but note that the expression "quantity of heat" is meaningful only in reference to an amount of energy that is transferred; a body cannot "contain" a quantity of heat anymore than it can contain a quantity of work. When heat is the only form of energy exchanged in an interaction between two or more systems (as in a mixing or calorimetry experiments), conservation of energy requires that the heat lost by the system(s) experiencing a decrease in temperature be equal to the heat gained by the system(s) experiencing an increase in temperature. Heat is often measured in units of calories (or kilocalories), but we shall try to consistently employ the joule unit (J), in accordance with the International System:
1 J ~ 1/4.2 cal = 1/4.2 x 103 kcal.
The units of specific heat are then joules per kilogram per degree (Kelvin or Celsius) of temperature change, or J/kg·K = J/kg°C.
EXAMPLE:
An aluminum block (c = 9.1 x 102 J/kg°C) of mass 0.80 kg at a temperature of 275°C is dropped into an aluminum calorimeter cup of mass 0.200 kg containing 1.00 kg of water (c = 4.2 x 103 J/kg°C) at 20°C. The system is insulated and attains equilibrium at a final temperature Tf.
Solution:
(a) Q "gained" by aluminum block = cAMA(Tf -TA)
Q gained by cup = ccMc(Tf -Tc)
Q gained by water = cwMw(Tf -Tw)
If Q total = 0, then
cAMA(Tf -TA) + ccMc(Tf -Tc) + cwMw(Tf -Tw) = 0
(b) Rearranging terms gives:
Tf(cAMA + ccMc + cwMw) = cAMATA + ccMcTc + cwMwTw
Tf = (cAMATA + ccMcTc + cwMwTw)/ (cAMA + ccMc + cwMw)
Tf = (2.878 x 105 J)/(5.1 x 103 J/°C) = 56°C
Note that heat is actually lost by the aluminum block, but this is
automatically taken into account by the fact that we wrote all temperature
changes as T(later) - T(earlier) in part (a), and put all of the heat terms on
one side of the equation. This differs slightly from the method used
where you set up the equation Q(gained) = Q(lost),
then you must be careful to make all T's positive,
that is, T(higher) -
T(lower). The results are the same--only the "bookkeeping" method is
different--but it is more customary to define a change in some quantity as the
final value minus the initial value.
Latent heat is the heat associated with the
transformation of a quantity of substance from one state or phase to a
different phase. For example, the quantity of heat absorbed by a unit mass of a
substance as it changes from the solid phase to the liquid phase at constant
temperature is the specific heat of fusion; this is equal in magnitude to the
amount of heat given up by a unit mass of the same substance as it changes from
liquid to solid at the same constant temperature. (The fact that phase changes
of pure substances occur at constant temperature was alluded to in the
preceding section when we mentioned the triple point of water as a reference
temperature: as long as ice, water, and water vapor coexist in a sealed
container, the temperature remains constant at 273.16 K.) It is useful to
introduce the idea of latent heat of transformation at this point to emphasize
that heat transfer doesn't always produce a temperature change
as in "mcT".
This equation is valid only when no other energy
transformations accompany the heat transfer. The following example illustrates
the analysis of a heat-transfer situation involving both a temperature change
and a phase change.
EXAMPLE:
A block of ice, mass 0.20 kg and temperature 0°C, is dropped into a brass calorimeter cup of mass 0.100 kg containing 0.300 kg of water at 80°C. Assuming that no heat is lost to the environment, use the following data to find Tf, the final equilibrium temperature.
cbrass = 4.2 x 102 J/kg°C; Lice melting = 3.3 x 105 J/kg; cwater = 4.2 x 103 J/kg°C.
Solution:
(a) Q1 = MiL + cwMi(Tf-0)
(b) Q2 = ccupMcup (Tf-80) + cwMw(Tf-80)
(c) 0= Q1 + Q2 = MiL + Tf(cwMi + ccupMcup + cwMw) - 80(ccupMcup + cwMw)
Tf= [80(ccupMcup + cwMw) - MiL]/ (cwMi + ccupMcup + cwMw) = ((3.816 x 104 J) / (2.142 x 103 J/°C) = 18°C
Problems:
Keywords: Heat; Thermal Transport; Conduction; Learning Objectives
OBJECTIVE:
The concept of heat conduction introduces a new proportionality factor which, like specific heat, is characteristic of a particular material and remains approximately constant over a relatively wide temperature range. The thermal conductivity, k, of a substance describes the rate at which heat energy will "flow" in the substance, in response to a unit temperature gradient, across a unit area in a plane perpendicular to the temperature gradient. Thermal conductivity has SI units of J/m·s·°C or, since 1 J/s = 1 W, of W/m°C. Note that the equation for the heat flow rate or heat current:
H = -kA (dT/dx),
is strictly applicable only under steady-state conditions, that is, where a heat current has been established that does not vary appreciably with time. Under these conditions, the heat flow is similar to the flow of an incompressible fluid; just as the equation of continuity requires that the same volume of fluid must move past any given section in a piper per unit of time, so must the same quantity of heat flow past each section of the heat conductor in response to a steady-state temperature gradient. The heat-flow equation also does not account for heat that is transferred by processes other than conduction, i.e., by radiation or convection. Despite these limitations, the equation provides a useful approximation in many cases of the rate at which heat energy will be transferred between two bodies maintained at different constant temperatures and separated by a specified conductor of given dimensions.
EXAMPLE:
A copper rod (length 0.35 m) has a circular cross section with radius r = 0.050 m . The two ends are kept at different, fixed temperatures, and the sides are insulated. The steady-state energy transfer along the rod is observed to be 8.4 x 102 W, and the temperature in the middle is 145°C. For copper the thermal conductivity k = 3.8 x 102 W/m K. What are the temperatures at the two ends of the rod?
Solution:
Since the rod has constant cross section, we can write the temperature gradient as
dT/dx = (T2 - T1)/L,
and the heat equation becomes
H = -kA(T2 - T1)/L or
(T2 - T1)=-(L/kA) H
Thus,
T2 - T1 = 0.35 m / [(3.8 x 102 W/m K)(2.50 x 10-3) m2)] x (8.4 x 102 W) = 98 K
and since the temperature is 145°C in the middle of the rod and varies linearly from one end to the other, we have:
T2 = 145 + 98/2 = 194°C;
T1 = 145 - 98/2 = 96°C.
Note: in the preceding example we have made use of the fact that the Kelvin and the Celsius degree are identical in size and are thus equivalent measures of temperature differences. When you see a number given with units of either K or °C, you must be careful to note whether it represents an actual temperature on the Kelvin or Celsius scale, or a temperature interval. In the latter case, the units are interchangeable; in the former, they clearly are not, since the zeros of the Kelvin and Celsius scales differ by 273.16 K.
Practice Exercises
IV. THE FIRST LAW OF THERMODYNAMICS
Keywords: The Laws Of Thermodynamics; The First Law Of Thermodynamics; Adiabatic Process; Isobaric Process; Isochoric Process; Internal Energy Of A System; Learning Objectives
OBJECTIVES:
PREREQUISITES:
Interpreting and evaluating an integral as the area under a curve. Calculating the work done by a constant or variable force; the kinetic energy of a particle, given its mass and velocity; or the change in gravitational potential energy of a particle moving near the earth's surface
Supplement:
We have already implicitly recognized the equivalence of heat energy and work (mechanical energy) when we adopted the joule as our unit of heat, and even earlier in our study of mechanics when we salvaged the law of energy conservation by asserting that mechanical energy "lost" to friction was actually converted to internal energy. The first law of thermodynamics is a quantitative, explicit statement of both energy conservation and the equivalence of work and heat. The first law can be stated in a number of forms, one of which is as follows:
For a given system that undergoes any process beginning and ending in equilibrium, the heat transferred to the system (Q) minus the work done by the system (W) is exactly equal to the change in the internal energy function U.In symbols,
Thermodynamics was originally the study of "heat engines", that is, systems that absorbed heat and performed work. Therefore, heat was naturally considered positive when it entered a system, and work was positive when it left the system. The same conventions are still used today, and this is the reason for the difference in sign between Q and W in the first law. It is important to be clear about the system under consideration and to define the boundaries of the system carefully. For example, if the system is a gas within a cylinder, the cylinder walls and the piston head form the boundaries. The size of the system or the shape of the boundary can change, as when the piston moves, but in applying the first law we must keep track of the heat and work crossing the boundary. For example, if the piston moves out, then the system does work W on the environment, and if a flame is put under the cylinder, then heat is transferred to the system. We shall consider only systems in which no material enters or leaves, or which can be idealized as such. It is possible to add a term to the first law to take into account matter entering or leaving the system, but this is taken up in more advanced courses. It is also important to note that the first law applies only to processes beginning and ending with the system in an equilibrium state. This is because our thermodynamic description of the system is based on state variables--pressure, volume, and temperature--that have unique values only when the system is in equilibrium. Thus, the change in internal energy,
U = Uf - Ui
is defined only when Uf and Ui are equilibrium states. The first law can also be written for infinitesimal changes as
dU = dQ - d/W.
The slashes below the differentials for Q and W indicate that these are not "exact differentials." This is to guard against any misconception that Q and W could be written as functions of (and thus be differentiated with respect to) any of the thermodynamic variables p, V, T,--there are no such functions. On the other hand, dU is an exact differential, and there does exist a unique function U that depends only on the state of the system and not on the path by which the system is brought to that state. Even though heat and work are not state functions, they may be calculated if we know something about the details of the process by which a system proceeds from one state to another state. Let us first consider the work performed by or on a thermodynamic system. You will recall that the general definition of the work done on a particle is
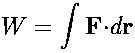
where the integral is carried out along the path taken by the particle. This definition can be written in terms of thermodynamic variables as
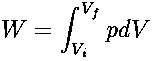
where p represents
the pressure within the system (which may, in general, vary in a complex way)
and the integral is carried out from the initial volume Vi
to the final volume
Vf.
(The vector F is the force on the world by the gas.)
Notice that work is positive when
the system expands (Vf > Vi),
but this tends to decrease the internal energy
function because of the minus sign in the first law. Since p may vary in
response to other factors as the volume of the system changes from Vi
to Vf, (p
is not, in general, a function of V alone) the value of the work integral is
often most easily interpreted as the area under the graph of p versus V.
Technically, this graph can be drawn only for a process that proceeds
quasi-statically, that is, through a sequence of equilibrium states. An
infinite number of graphs can be drawn for given values of Vi
and Vf, with each
graph corresponding to a different sequence of states and, in general,
different quantity of work performed by the system. It is important to remember
that the internal energy of a system can also change as a result of work that
is not associated with a volume change. For example, electrical and frictional
forces can also do work, and this must be included in calculating
U. Negative
work--that is, work done on the system by the environment--has the effect of
increasing the internal energy function. Thus, rapidly rubbing your hands
together raises the temperature of your palms, and vigorous stirring of a
water-ice mixture causes some of the ice to melt. The second way that the
internal energy of a system can be changed is through the mechanism of heat
transfer or heat flow; this does not involve the performance of work but rather
is associated solely with a difference in temperature across the boundary
separating the system and the environment. For example, you could warm your
hands by holding them near a fire, and ice will melt when a container holding a
water-ice mixture is set on top of a radiator. In each case, the transfer of
energy associated with a difference in temperature brings about changes in
system properties, and these changes are exactly the same as would be produced
by the performance of an equivalent amount of work.
In this lesson, you have
studied three topics related to heat transfer: heat conduction, specific heat
capacity, and change of phase. These are basically just ways of accounting for
or measuring the heat, Q, transferred across the boundary of a system; thus,
they provide a way to put numbers into the first law. For example, for a pot of
water on the stove, we can calculate Q in three different ways: (1) The
temperature difference T between the inside and outside
of the bottom, plus
its thermal conductivity k, thickness L, and area A
lead to a value for
H =
T/L).
(2) If the water temperature is observed to rise by T,
then Q can be found from Q = mcT,
where m represents the mass of water in the
pot, and c represents the known specific heat capacity of water. (3) If the
water is allowed to boil and M kg changes to steam, then, using L to represent
the known heat of vaporization of water, we have Q = ML.
Since work and heat
produce identical changes in internal energy, the latter two of these
relationships can be used to calculate the temperature change or quantity of a
substance that changes phase as a result of work done on or by the system, as
well as changes that result from heat transfer. Remember that mechanical
energy, the sum of kinetic and potential energy, can be converted into internal
energy in various ways, always through the performance of work. If
nonconservative forces of known magnitude act through known distances, then the
energy transferred from mechanical to internal form can be calculated from the
definition of work. Generally, though, it is simpler to calculate initial and
final mechanical energies directly, and identify the difference as the change
in internal energy.
EXAMPLE:
A block of ice at 0°C with mass 50 kg, slides along a horizontal surface, starting at a speed of 5.4 m/s and finally coming to rest after traveling 28.3 m. Given the coefficient of sliding friction µ, calculate the heat generated and, assuming that all of the heat is transferred to the ice, the mass of ice melted.
Solution:
Rather than calculating the work using the weight, coefficient of friction, and distance traveled, we note that all of the initial kinetic energy is converted into internal energy of the ice.
K = (1/2) m1v2,
where m1 = 50 kg, and v = 5.4 m/s. Thus
K = (1/2)(50 kg)(5.4 m/s)2 = 730 J.
Now, Uice = m2L
, where m2 represents the mass of ice melted, and L = 3.3
x 105 J/kg, the heat of fusion for water. We set
Uice = K , or
m2L = 730 J, and
find:
m2 = 730 J / 3.3 x 105 J/kg = 2.10 x 10-3 kg.
This is a very small amount of ice melted. In general, the amounts of mechanical energy with which we have direct experience (102 to 103 J) produce rather small thermal effects.
EXAMPLE
A waterfall is 75 m high. The water has a temperature of 20.0°C above the waterfall and is flowing at 4.0 m/s. Calculate the expected temperature at the bottom. Start from the first law; neglect any transfer of heat to the ground or to the air. Water has a density of 103 kg/m3 and a specific heat of 4.2 x 103 J/kg K.
Solution:
U = Q - W.
The system is a given mass of water. Q = 0, since we are neglecting heat transfer to the ground and air. The work is done on the system by the earth and the surrounding water; therefore W is negative and is equal in magnitude to the increase in internal energy. If we take the mechanical energy of the water to be zero at the bottom of the waterfall, we can calculate W by equating it with the kinetic plus gravitational potential energy of the water at the top of the waterfall:
-W = Ei
- Ef = [(1/2)mv2 + mgh] - 0 =
U.
To calculate the temperature rise associated with this change in internal energy, we use the definition of specific heat,
U= cmT =
(1/2)mv2 + mgh;
T = [(1/2)v2 + gh]/c =
0.18°C.
We thus expect a temperature of 20.18°C; gain, the very small thermal effect of even this relatively large amount of work would be difficult to measure. (Joule actually tried this experiment, unsuccessfully.)
You should be familiar with
three terms used to describe particular types of thermodynamic processes: An
adiabatic process is one in which Q = 0. This is usually the result of
insulation surrounding the system of interest, but a process can also occur
quickly enough so that no appreciable amount of heat can be transferred to or
from the working substance, and such a process is also referred to as
adiabatic. Examples of the latter type include the expansion of the burning
gases in an automobile engine cylinder, and the compression of air in a sound
wave. For adiabatic processes, U = -W.
An isobaric process is carried out at
constant pressure. All processes carried out with systems open to the
atmosphere are isobaric. For an isobaric process,
W = p(V);
thus, if a volume change occurs as part of an isobaric process, the work is easy to calculate. In an isometric (or isochoric) process, the volume of the system remains the same. Since Vi = Vf,
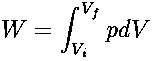
and no external work is performed by the system (W = 0). These terms are especially useful in reference to pV graphs for idealized processes; to draw (or interpret) a pV graph for a process, we must know the conditions for each segment of the path that the process follows:
EXAMPLE:
Solution:
(a)
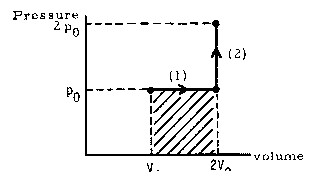
Recalling that the work done by the system in a process is the area under its pV graph (or the negative of this area if the process proceeds from right to left) we see that
W1 = p0(2V0 - V0) = p0V0
represented by the shaded area in the graph, and
W2 = 0
which we could have concluded immediately from the fact that step (2) is an isochoric process.
Having considered some of the basic implications of the first law, let us now work through a more extended example that involves the analysis of a multistep, quasistatic process.
EXAMPLE:
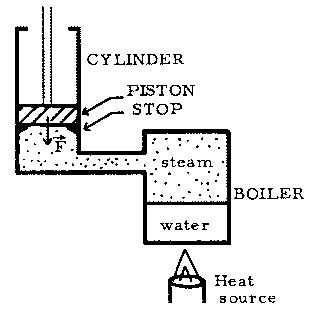
The above figure is a schematic of a primitive form of steam engine, the Newcomen engine. [You may be interested to know that this engine once represented the vanguard of technology, and it was used for some time to pump water out of the mines of England, in spite of its shocking inefficiency (by today's standards). Its success and its defects provided the stimulus for James Watt to invent a more efficient steam engine.] The operation of this engine can be idealized as follows.
Stage 1: Isochoric heating--heat Q1 flows into the boiler and changes some of the water to steam, gradually increasing the gauge pressure on the bottom of the piston from 0 to p1. (The piston is initially held against the stops by a constant force F, resulting from the weight of the piston and the atmospheric pressure on the top of the piston.)
Stage 2: Isobaric expansion--when the boiler pressure reaches
p1, then the upward force just balances F, and the piston rises slowly. The
pressure of the system remains constant as heat Q2 is absorbed and the volume
of the system increases from V1 to V2.
Using the following data:Q1 = 2.10 x 105
J, Q2 = 2.90 x 105 J; p1 = 4.0 x 105 Pa,
V1 = 0.100 m3, and V2 = 0.200 m3,
(a) Draw a pressure-volume graph for Stages 1 and 2; (b) give the value of W1,
the work done during Stage 1; (c) find the value of U1, the change in internal
energy in Stage 1; (d) calculate W1, the work done during Stage 2, justify the
sign of the answer, and identify the area on the pV graph corresponding to W2;
(e) calculate U2, the change in internal energy during Stage 2, and justify
the sign of the answer; (f) evaluate W, Q, and U for the complete process
(Stage 1 plus Stage 2).
Solution:
(a) See Figure
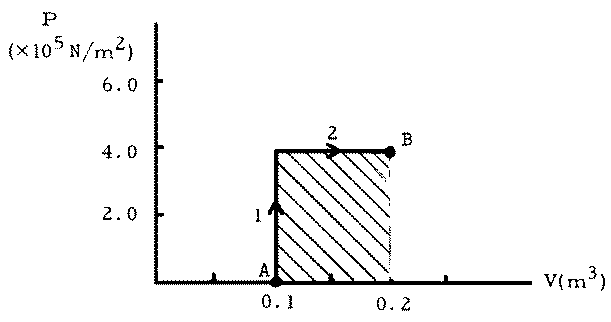
(b) W1 = 0 (because V = 0).
(c) U1 = Q1 - W1 =
Q1 = 2.10 x 105 J.
(d) W2 = p V =
(4.0 x 105 Pa)(0.200 - 0.100) m3 = 4.0 x 104 J.
This corresponds to the shaded area in the graph and is positive because the system expanded and did work on the environment.
(e) U2 = Q2 - W2 =
(2.90 x 105 J) - (4.0 x 104 J) = 2.50 x 105 J.
This is positive because the system gained more energy by heat flow than it lost by doing work.
(f) Wtotal = W1 + W2 = 4.0 x 104 J;
Qtotal = Q1 + Q2 = 5.0 x 105 J.
Utotal = U1 +
U2 = 4.6 x 105 J.
Note that if the final state B were
reached by means of a different path, say the straight line from A to B, we
would obtain different values for W and Q but the same result for U.
Practice Exercises:
V, during isobaric vaporization.
calculate the work done by the system on the surrounding atmosphere. Is this work positive or negative?
U.
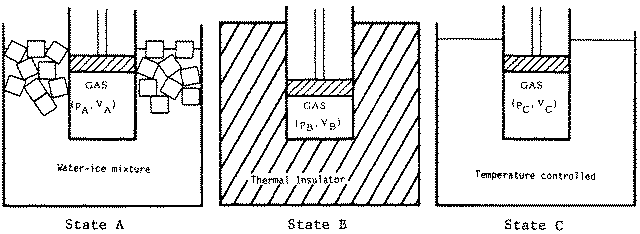
The cylinder is initially immersed in a water-ice mixture, and the gas is in thermal equilibrium with pressure pA = 1.50 x 105 Pa and volume VA = 0.0140 m3. We shall refer to this as State A of the system. The gas then undergoes the following sequential changes:
Process 1: The cylinder is removed from the ice-water bath, surrounded with an insulating jacket, and the piston is gradually pushed in. In other words, the gas is compressed adiabatically. The final state of the gas is now State B (see pV graph) with pressure pB = 3.6 x 105 Pa and volume VB = 8.3 x 10-3 m3. During this process the gas has done work W1.
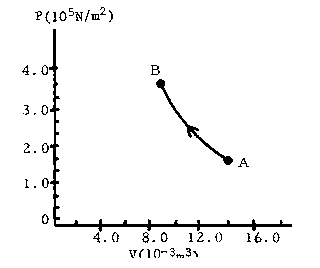
Process 2: The temperature of the gas is measured, and the cylinder is placed in a controllable bath at the same temperature. The piston is now allowed to move out gradually, and the temperature of the bath (and thus the gas) is controlled in such a way as to keep p = -kV + c, with k and c constant. This process is continued until the piston is at the same position as in State A, and the gas is said to be in State C, at a pressure of pC = 2.40 x 105 Pa and volume VC = VA. During Process 2 the gas does work W2 and gains heat Q2.
Process 3: The piston is fixed in place; the cylinder is placed back in the ice-water mixture and is allowed to come to thermal equilibrium, thus completing a closed cycle. During Process 3, the heat flow is Q3 and the work done is W3. See Figure
(a) Process 1 and States A and B are shown on the pV graph above.
Show Processes 2 and 3 and State C on this graph. (b) Calculate W2. (c)
Suppose that during Process 2, the net heat gained from the bath is Q2 = +3040
J. Calculate the change in the internal energy function during Process 2,
U2.
(d) Suppose that during Process 3, 5.7 x 10-3 kg of ice melted in the bath.
Using L = 3.30 x 105 J/kg, calculate Q3. (e) Find the change in internal
energy during Process 3, U3. (f) Find the change in internal energy during
Process 1, U1. Hint: Use the results of (c) and (e). (g) Using the result of
(f), find W1. (h) Combine your results for W1,
W2, and W3 to find the total
work done during the cycle. (i) Combine your results for Q1,
Q2, and Q3 to
find the total heat added during the cycle. (j) Combine the results for W1,
W2, and W3 and Q1,
Q2, and Q3 to determine whether, over the entire cycle, work
input is being converted to heat output or heat input is converted to work
output. How many joules of heat (or work) is converted over the entire
cycle?
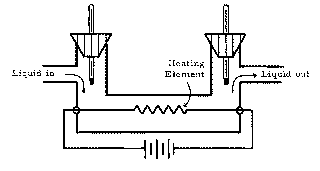
A liquid of density 1200 kg/m3 flows through at the rate of 1.20 x 10-5 m3/s. The heating element supplies 400 W, and, after steady state is achieved, it is observed that the liquid flowing out is 20.0° warmer than the liquid entering. (a) Assume that no heat is lost to the environment, and consider the mass of liquid flowing through the system in t seconds to be the system. Set up an equation for Q1 (the amount of heat gained by this system in time t) in terms of M (the mass of liquid flowing through in time t), c (the specific heat of the liquid), and T (the temperature change of the liquid). (b) Find Q2, the amount of heat lost by the heating element in t seconds. (c) Using the results of (a) and (b), set up the Q1 + Q2 = 0 equation, solve for the specific heat capacity, and evaluate the resulting expression.
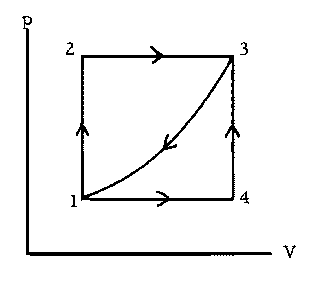
In the process 1 
2 3,
90 J of heat enters the system, and 40
J of work is done by the system. In the process 1
4 3, 10.0 J
of work is done by the system. In the direct process 3 1, the amount
of work is 22.0 J. (a) How much heat enters or leaves the system in the
process 1 4 3?
(b) How much heat enters or leaves the system
during the direct process 3 1? (c) How much work is done during the
cycle 1 2 3
1? (d) If U12 = 30.0 J, how much work
is done during the process 1 2, and how much heat enters or leaves the
system?