Orbits in 3D

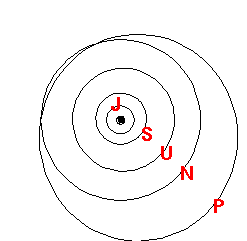
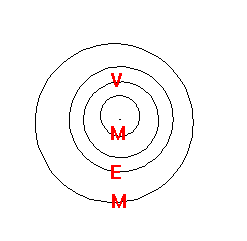
In many pictures of the orbits of the planets it seems that Pluto and Neptune might collide...is this possible?

QuickTime movie of Solar System orbits (0.5 MB)

If you view the above movie you see that the orbital inclination of Pluto compared to the rest of the planets, means collision is avoided.

We consider here the orientation of elliptical orbits in our three dimensional world. Orbits are no different from any object: they can be twisted and turned in space. How many angles does it take to describe all possible orientations of an object? Three: for example: two angles to specify the axis of rotation and one angle to specify the amount of rotation about that axis. The credit for inventing three useful angles to describe orientation if given to:

Leonhard Euler "Oiler" (1707-83) Born in Basel, student of the Bernoullis, Euler answered the call of such notables at Fredrick the Great and Catherine the Great and thus worked at various locations around Europe. In addition to Euler angles, described below, we mention Euler's Theorem (which we used above): the most general displacement of a rigid body with one fixed point is a rotation about some axis.

We start our reorientation of an ellipse with the orbit in a standard position:

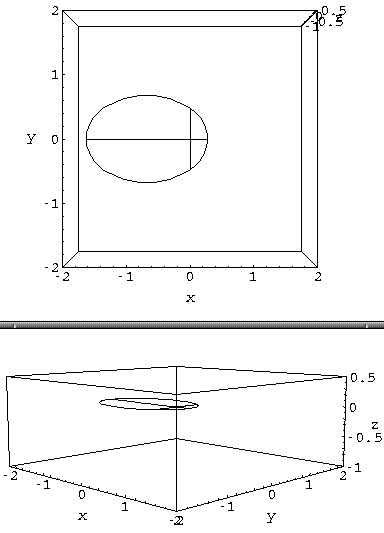
In this snapshot, the top frame shows the view looking down the z-axis and the bottom frame shows the view from a point a bit above the y=-x line. The major axis lies along the x-axis, the orbital plane is the x-y plane, and the angular momentum is along the +z axis.

We now rotate the orbit about the z-axis by an angle known as the argument of perihelion, 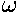. (In more general treatments of rigid body motion, this would be called the angle .)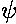

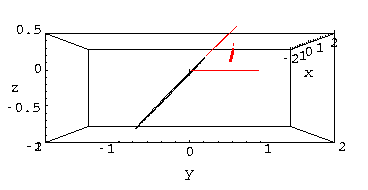
The orbit is now tilted up by rotating it along the x axis. This angle is know as the inclination, i. (In more general treatments of rigid body motion, this would be called the angle 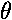.) Note that after tilting, the orbit intersects the x-y plane only along a line, known as the line of nodes

It is hard to see this tilt in our standard views. Here is the view along the x-axis:

Finally we again rotate along the z-axis. The line of nodes, which was along the x-axis, is now at some angle 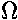, known as the longitude of the ascending node

Note that in systems (like the Solar System) in which the inclinations of the orbits are small, it is hard to separate 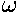from 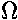, so another angle, the longitude of perihelion 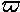(this is an alternative form of the greek letter 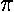and so is pronounced "pi").

= +

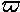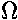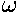
QuickTime movie of Orbit Orientation (0.8 MB)

In Mathematica we can make orbits in 3D:

<<Geometry/Rotations.m
a=1; e=.707
ParametricPlot3D[Evaluate[
    RotationMatrix3D[-omega,-i,-nodes].{ a(Cos[u]-e), a Sqrt[1-e^2] Sin[u], 0 }
    ],{u,-Pi,Pi},
    AxesLabel->{x,y,z},ViewPoint->{2,-2,.4}]

r=(a(cos(u)-e), a (1-e²)^½ sin(u), 0)

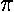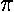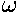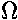where - < u < is the eccentric anomaly, omega= (the argument of perihelion) i=i (the inclination) node= (the longitude of the ascending node)