The Kolmogorov-Smirnov test (KS-test) tries to determine if two datasets differ significantly. The KS-test has the advantage of making no assumption about the distribution of data. (Technically speaking it is non-parametric and distribution free.) Note however, that this generality comes at some cost: other tests (for example Student's t-test) may be more sensitive if the data meet the requirements of the test. In addition to calculating the D statistic, this page will report if the data seem normal or lognormal. (If it is silent, assume normal data at your own risk!) It will enable you to view the data graphically which can help you understand how the data is distributed.
Click here to enter data for the KS-test
The process of assigning numbers to results is not straightforward. There is no fairy god mother that can wave her magic wand and tell you if results are evidence for or against an effective treatment. One simple strategy you might have thought of is surely dead wrong: try lots of different statistics and pick the one that reports want you want. (Bill Gates will soon automate this process; coming soon: the "click here to try all tests" button.) Let me explain why. Every statistical test makes "mistakes": tells you the treatment is effective when it isn't (type I error) or tells you the treatment is not effective when it is effective (type II error). These mistakes are not user-errors, rather the statistical tool --properly used and applied to real data-- simply lies some small fraction (say a few percent) of the time. Thus if you apply many different statistical tests you are very likely to get at least one wrong answer.
Statisticians, of course, try to make statistics that only rarely (say 5% of the time) lie. In doing this they tune their tests to be particularly good at detecting differences in common situations. Used in those situations the tests may be the best possible tests. Used in different situations the tests may lie outrageously. For example, Student's t-test assumes that the situations produce "normal" data that differ only in that the average outcome in one situation is different from the average outcome in the other situation. If you apply the t-test to non-normal data, you are probably increasing the risk of error. Now, in fact, the Central Limit Theorem shows that the t-test can avoid becoming unusually fallible when applied to non-normal datasets: If the control/treatment datasets are sufficiently "large" the t-test does not lie outrageously even when applied to non-normal data. Thus the t-test is called a "robust" test, since it continues to work well in situations different from those narrow situations for which it was created. This is important because users of statistical tests often do not know if their dataset meets the criteria intended by the creator of the statistical test.
There are then a few situations in which it is a mistake to trust the results of a t-test:
controlA={0.22, -0.87, -2.39, -1.79, 0.37, -1.54, 1.28, -0.31, -0.74, 1.72, 0.38, -0.17, -0.62, -1.10, 0.30, 0.15, 2.30, 0.19, -0.50, -0.09}
treatmentA={-5.13, -2.19, -2.43, -3.83, 0.50, -3.25, 4.32, 1.63, 5.18, -0.43, 7.11, 4.87, -3.10, -5.81, 3.76, 6.31, 2.58, 0.07, 5.76, 3.50}
Notice that both datasets are approximately balanced around zero; evidently the mean in both cases is "near" zero. However there is substantially more variation in the treatment group which ranges approximately from -6 to 6 whereas the control group ranges approximately from -2½ to 2½. The datasets are different, but the t-test cannot see the difference.
controlB={1.26, 0.34, 0.70, 1.75, 50.57, 1.55, 0.08, 0.42, 0.50, 3.20, 0.15, 0.49, 0.95, 0.24, 1.37, 0.17, 6.98, 0.10, 0.94, 0.38}
treatmentB= {2.37, 2.16, 14.82, 1.73, 41.04, 0.23, 1.32, 2.91, 39.41, 0.11, 27.44, 4.51, 0.51, 4.50, 0.18, 14.68, 4.66, 1.30, 2.06, 1.19}
These datasets were drawn from lognormal distributions that differ substantially in mean. The KS test detects this difference, the t-test does not. Of course, if the user knew that the data were non-normally distributed, s/he would know not to apply the t-test in the first place.
One of the advantages of the KS-test is that it leads to a graphical presentation of the data, which enables the user to detect normal distributions (see below). For larger datasets (say N>40), the Central Limit Theorem suggests that the t-test will produce valid results even in the face of non-normally distributed data. However, highly non-normal datasets can cause the t-test to produce fallible results, even for large N datasets. In the last example you will see a case where the t-test fails at N=80.
controlB={1.26, 0.34, 0.70, 1.75, 50.57, 1.55, 0.08, 0.42, 0.50, 3.20, 0.15, 0.49, 0.95, 0.24, 1.37, 0.17, 6.98, 0.10, 0.94, 0.38}
it is hard to see the general situation. Thus descriptive statistics were developed to reduce the list of all the data items to a few simpler numbers. Thus we can perhaps better interpret data set from the following:
Mean = 3.61
Median = 0.60
High = 50.6 Low = 0.08
Standard Deviation = 11.2
We can see from this that something is abnormal. For normally distributed data you should expect about 15% of the data to lie more than 1 standard deviation below the mean (i.e., below 3.61-11.2=-7.59), but no data are that small, in fact no datum is even negative. Similarly only about 2% of the data should be more than 2 standard deviations above the mean (i.e., above 3.61+2×11.2=26.01), but in fact we have one data-point (50.57) way beyond that (hence an "outlier"). Something is funny about the distribution of this data; we need a way to look at how the data is distributed.
sorted controlB={0.08, 0.10, 0.15, 0.17, 0.24, 0.34, 0.38, 0.42, 0.49, 0.50, 0.70, 0.94, 0.95, 1.26, 1.37, 1.55, 1.75, 3.20, 6.98, 50.57}
Evidently no data lies strictly below 0.08, 5%=.05=1/20 of the data is strictly
smaller that 0.10, 10%=.10=2/20 of the data is strictly smaller than
0.15, 15%=.15=3/20 of the data is strictly smaller than
0.17... There are 17 data points smaller than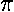 
, and hence
we'd say that the cumulative fraction of the data smaller
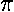than is .85=17/20. For any number x,
the cumulative fraction
is the fraction of the data that is strictly smaller than x.
Below is the plot of the cumulative fraction for our control
data. Each step in the plot corresponds to a data-point.
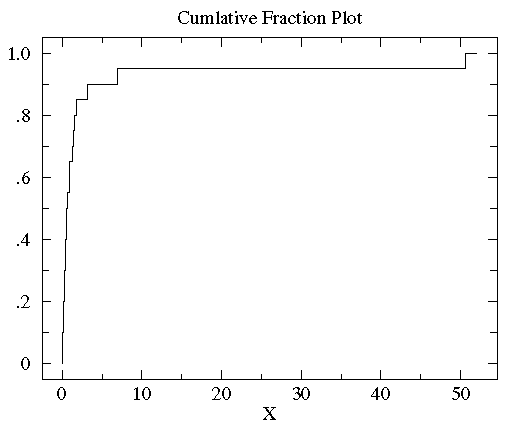
You can see with a glance that the vast majority of the data is scrunched into a small fraction of the plot on the far left. This is a sign of a non-normal distribution of the data. In order to better see the data distribution, it would be nice to scale the x-axis differently, using more space to display small x data points. Since all the data are positive you can use a "log" scale. (Since the logarithm of negative numbers and even zero is undefined, it is not possible to use a log scale if any of the data are zero or negative.) Since many measured quantities are guaranteed positive (the width of a leaf, the weight of the mouse, [H+]) log scales are common in science. Here is the result of using a log scale:
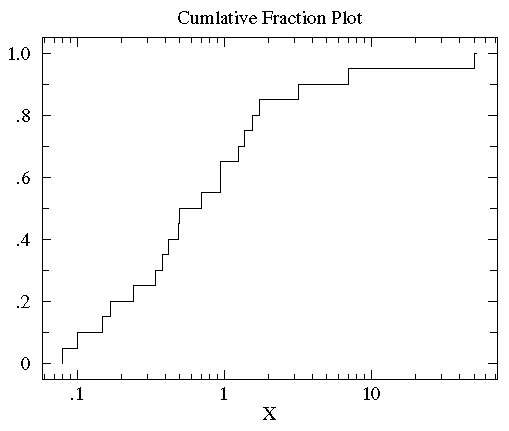
You can now see that the median (the point that divides the data set evenly into two: half above the median, half below the median) is a bit below 1.
We now plot the cumulative fraction of the treatment group on the same graph as we plotted the control cumulative fraction. (We'll use a dashed line to display the treatment group so we can distinguish it from the control group.)
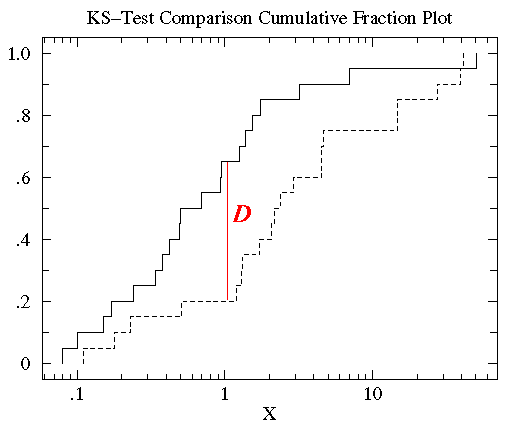
You can see that the control and treatment datasets span much the same range of values (from about .1 to about 50). But for most any x value, the fraction of the treatment group that is strictly less than x is clearly less than the fraction of the control group that is less than x. That is, by-and-in-large the treatment values are larger than the control values for the same cumulative fraction. For example, the median (cumulative fraction =.5) for the control is clearly less than one whereas the median for the treatment is more than 1. 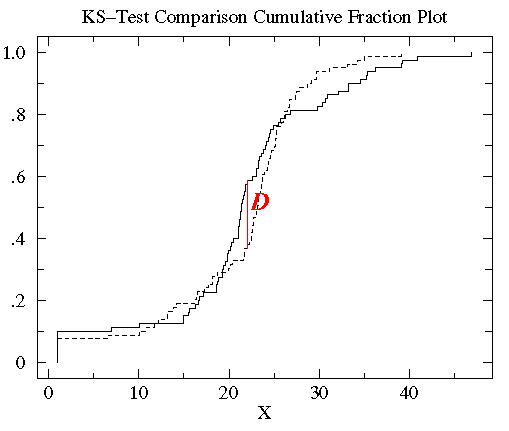The KS-test uses the maximum vertical deviation between the two curves as the statistic D. In this case the maximum deviation occurs near x=1 and has D=.45. (The fraction of the treatment group that is less then one is 0.2 (4 out of the 20 values); the fraction of the control group that is less than one is 0.65 (13 out of the 20 values). Thus the maximum difference in cumulative fraction is D=.45.)
Note that unlike the t-statistic, the value of the D statistic (and hence the P value) is not affected by scale changes like using log. The KS-test is a robust test that cares only about the relative distribution of the data. In the above case, use of the log scales just moved the important region so the user could see the distribution of the data.
In a similar way we can examine the data in the first example:
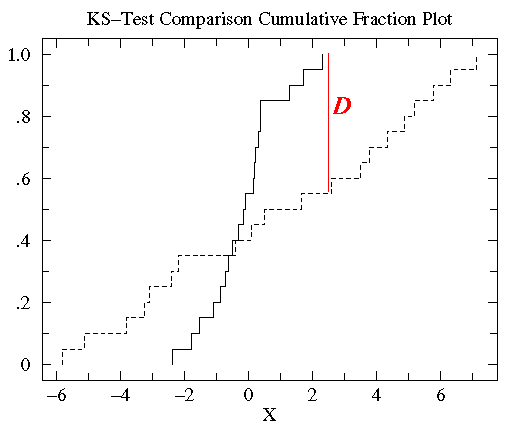
Again, with a glance you can see that the treatment group has more variation than the control group, but a similar median. 100% of the control group is less than 2.31 whereas only 55% of the treatment group is below 2.31. Thus D=.45, and the corresponding P value suggests a significant difference.
{-0.45, 1.11, 0.48, -0.82, -1.26}
we can sort this data from smallest to largest:
{ -1.26, -0.82, -0.45, 0.48, 1.11 }
The exact middle data-point (-0.45) is called the median, but it is also the 50th-percentile or percentile=.50. Note that at x=-0.45 the cumulative fraction makes a step from .4 to .6. The percentile value will always lie somewhere in the step region. In general the percentile is calculated from the point's location in the sorted dataset, r, divided by the number of data-points plus one (N+1). Thus in the above example, the percentile for -.45 is 3/6=.5. In summary:
percentile = r/(N+1)
Thus we have the following set of (datum,percentile) pairs:
{ (-1.26,.167), (-0.82,.333), (-0.45,.5), (0.48,.667), (1.11,.833) }
We can connect adjacent data points with a straight line. (The resulting collection of connected straight line segments is called a ogive.) The below plot compares the percentile plot (red) to the cumulative fraction.
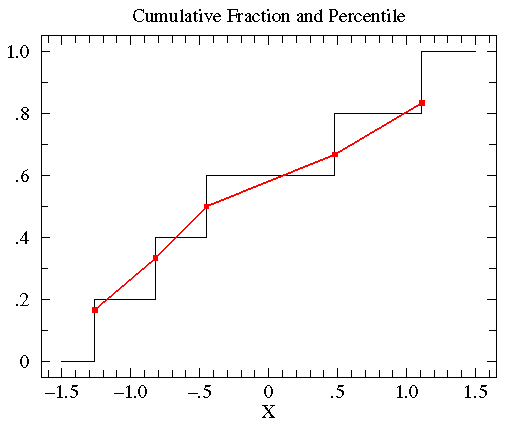
There are a couple of reasons for preferring percentile plots to cumulative fractions plots. It turns out that the percentile plot is a better estimate of the distribution function (if you know what that is). And plotting percentiles allows you to use "probability graph paper"...plots with specially scaled axis divisions. Probability scales on the y-axis allows you to see how "normal" the data is. Normally distributed data will plot as a straight line on probability paper. Lognormal data will plot as a straight line with probability-log scaled axes. (Incidently uniformly distributed data will plot as a straight line using the usual linear y-scale.)
The KS-test reported the treatmentB data in the second example was approximately lognormal with geometric mean of 2.563 and multiplicative standard deviation of 6.795. In the below plot, I display the percentile plot of this data (in red) along with the behavior expected for the above lognormal distribution (in blue).
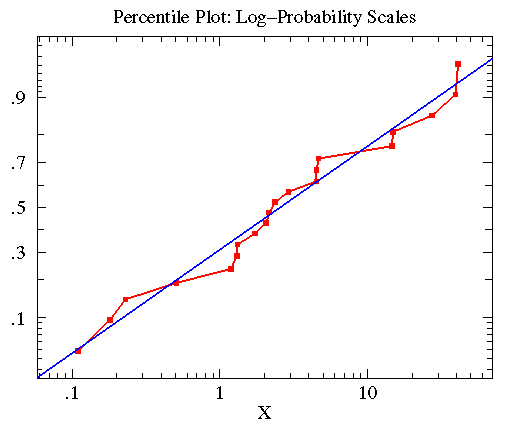
Note that the KS-test reports that both treatmentB and controlB data are approximately lognormal. Thus you could take the log of all the data, and use the resulting data in a t-test. Since the t-test is a quite sensitive test when applied to appropriate data this would be the best strategy.
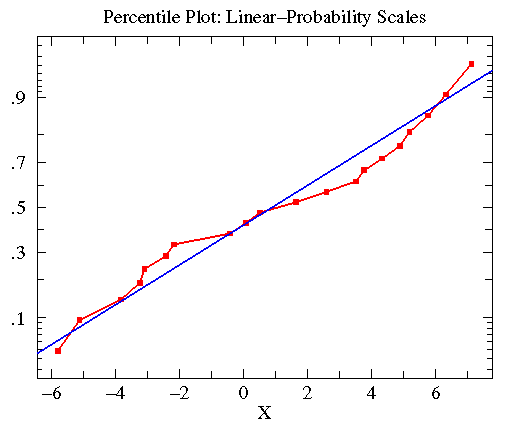
Similar consideration of the treatmentA data in the first example lead to the following plot. Here the KS-test reported that the data was approximately normally distributed with mean=.8835 and standard deviation=4.330 (plotted in blue).
redwell={23.4, 30.9, 18.8, 23.0, 21.4, 1, 24.6, 23.8, 24.1, 18.7, 16.3, 20.3, 14.9, 35.4, 21.6, 21.2, 21.0, 15.0, 15.6, 24.0, 34.6, 40.9, 30.7, 24.5, 16.6, 1, 21.7, 1, 23.6, 1, 25.7, 19.3, 46.9, 23.3, 21.8, 33.3, 24.9, 24.4, 1, 19.8, 17.2, 21.5, 25.5, 23.3, 18.6, 22.0, 29.8, 33.3, 1, 21.3, 18.6, 26.8, 19.4, 21.1, 21.2, 20.5, 19.8, 26.3, 39.3, 21.4, 22.6, 1, 35.3, 7.0, 19.3, 21.3, 10.1, 20.2, 1, 36.2, 16.7, 21.1, 39.1, 19.9, 32.1, 23.1, 21.8, 30.4, 19.62, 15.5}
whitney={16.5, 1, 22.6, 25.3, 23.7, 1, 23.3, 23.9, 16.2, 23.0, 21.6, 10.8, 12.2, 23.6, 10.1, 24.4, 16.4, 11.7, 17.7, 34.3, 24.3, 18.7, 27.5, 25.8, 22.5, 14.2, 21.7, 1, 31.2, 13.8, 29.7, 23.1, 26.1, 25.1, 23.4, 21.7, 24.4, 13.2, 22.1, 26.7, 22.7, 1, 18.2, 28.7, 29.1, 27.4, 22.3, 13.2, 22.5, 25.0, 1, 6.6, 23.7, 23.5, 17.3, 24.6, 27.8, 29.7, 25.3, 19.9, 18.2, 26.2, 20.4, 23.3, 26.7, 26.0, 1, 25.1, 33.1, 35.0, 25.3, 23.6, 23.2, 20.2, 24.7, 22.6, 39.1, 26.5, 22.7}
This example is based on data distributed according to the Cauchy distribution: a particularly abnormal case. The plots do not look particularly abnormal, however the large number of outliers is a tip off of a non-normal distribution. The web page is silent on if this data is normal or lognormal; that means it finds no evidence for either possibility. This relatively large sample size can not save the t-test: it cannot see the difference, whereas the KS-test can. The t-test is not robust enough to handle this highly non-normal data with N=80.
