 = a A2 + b AB +
c B2 + d A + e B + f
= a A2 + b AB +
c B2 + d A + e B + f
 = a A2 + b AB +
c B2 + d A + e B + f
= a A2 + b AB +
c B2 + d A + e B + f
so the constant χ2 curves are ellipses. Parameter error determination depends on understanding the region where χ2 is near its minimum value, for example:
χ2(a,b) ≤ χ2min + 1
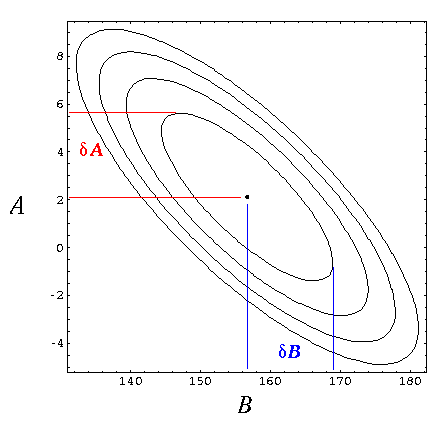
In particular we need to find the maximum reach of these ellipses, for example δA and δB shown below:
If we shift the origin for the parameters a and b to be at the center of the ellipse, using:
Δb = B - Bcenter
the quadratic form can be simply expressed as a matrix equation:
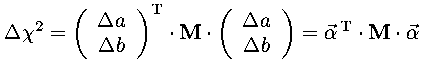
We then generalize that a bit to include N re-origined parameters αi put together into a column vector.
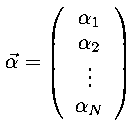
The symmetric matrix M is called the curvature matrix. In those cases where χ2 is a simple quadratic form, this result is exact. More generally we can view this equation as the first non-zero term in a Taylor expansion of Δχ2 at the minimum. M is then closely related to the matrix of second partial derivatives of χ2 (which is known as the Hessian). We will soon have use for the inverse of the matrix M, which is known as the covariance matrix.
The points we seek (the extreme reach of these ellipses) may be identified by gradient of χ2 (wrt the parameters αi): at the extreme points the gradient points directly along the corresponding coordinate axis as shown below:
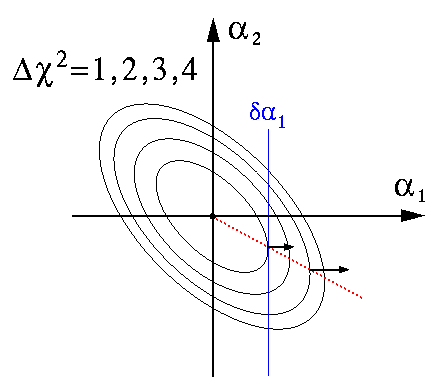
Note that because all the ellipses are self-similar, the extreme points all lie along a ray (shown in dotted red above).
The gradient of χ2 is:
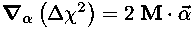
so the requirement that the gradient points directly along the pth coordinate axis amounts to the equation:
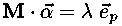
where ep is the unit vector in the pth coordinate direction (e.g., e1=(1,0,...,0), e2=(0,1,0,...,0), etc.) and λ is the length of the vector. We can find the locations where the gradient is along the pth coordinate direction, by inverting the above equation:
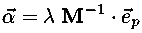
the result is a ray of locations parametrized by λ with larger λ corresponding to larger values of the associated Δχ2 ellipse. If we substitute the equation for this ray into the equation for Δχ2 we can associate the value of λ with the corresponding value of Δχ2:
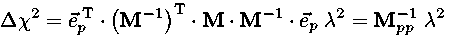
so
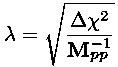
and
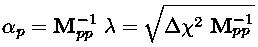
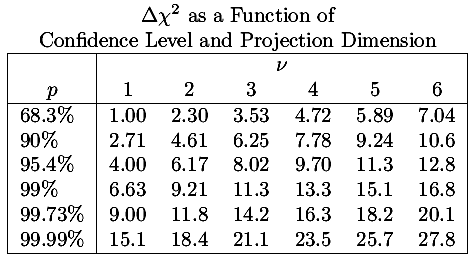
As noted above, generally we are interested in Δχ2=1, hence the mantra: the error in a parameter is the square root of the corresponding diagonal element of the covariance matrix. However I reproduce below a table from Numerical Recipes which at least shows that sometimes other values of Δχ2 may be of interest.