Descriptive Statistics
Click here to calculate using copy & paste data entry
They are different, but not different enough to matter --
like the maple leaves off the tree in my yard, when all I want to do is
rake them up.
Roald Hoffmann, 1981 Nobel Laureate in Chemistry
from: The Same and Not the Same
If you were to measure the size of 10 maple leaves you would quickly
find that maple leaves in fact come in different sizes. Thus it is
impossible to report the size of maple leaves, instead the
best you can do is to report a typical size and give some estimate
of the range of variation above and below that typical size.
The attempt to capture the full meaning of "the size of maple
leaves" in a few numbers is bound to fail -- Nature really
is more complex than our descriptions of it. Nevertheless
if our choice is to be silent on "the size of maple
leaves" or to provide a list of the size of every maple
leaf in the world (on this day) or to provide a few summarizing
numbers, the latter is the option selected by science. This page introduces a handful
of statistics which are commonly used to describe the distribution
of data.
Typical Values
There are several common methods of selecting a "typical" value
for data. The most common method is the average or
mean. To obtain an average value, add up all your data
values and divide by the number of data items. If X01
is the length of your first maple leave, X02
the length of your second maple leave, etc., then the average maple
leaf length is:
(X01+X02+X03+
X04+X05+X06+
X07+X08+X09+
X10)/10 = Xavg
To obtain the median value, first sort your list of leaf-lengths
from lowest to highest:
{5.1, 7.2, 4.1, 9.5, 6.7, 7.8, 8.5, 7.0, 7.3, 9.0} becomes:
{4.1, 5.1, 6.7, 7.0, 7.2, 7.3, 7.8, 8.5, 9.0, 9.5}
and then select the value in the exact middle as the median. (It turns
out that if the number of items is even, as in this example,
there is no exact middle. 7.2 is 5 places from the front and
6 places from the back; 7.3 is 6 places from the front and 5 places
from the back. So with even-numbered data sets, average the two
near-middle values, producing Xmed=7.25 in this example.)
The mode "typical" value will be of less use to us:
it is the most repeated value in the data set. In the above
example, no value is repeated (each value occurs exactly once).
This is commonly the case with so few data items; hence its limited
utility for us.
The geometric mean is useful for "log-normal distributions".
To obtain the geometric mean, multiply all the numbers together
and then take the result to the power 1/N (where N
is the number of data items -- 10 in our example). So the geometric
mean is:
(X01·X02·X03·
X04·X05·X06·
X07·X08·X09·
X10)1/10 = Xgeo
Estimates of the Range of Variation
In some sense, the range of variation is limited only by your
willingness to search through ever larger piles of leaves.
Generally, the more data you record the more extreme your highs
and lows will be. Nevertheless, you should find that the range
of leaf lengths, that includes say 50% of your sample, remains
about the same even if you look through ever larger piles of leaves.
That is to say, there is a common range of variation even as larger
data sets produce rare "outliers" with ever more extreme deviation.
Estimates of the range of variation seek to put a number to this
common range of variation that doesn't depend on sample size.
The most common way to describe the range of variation is
standard deviation (usually denoted by the Greek letter
sigma:  ). The standard deviation is simply
the square root of the variance, so lets start by describing
the variance. To obtain the variance start by subtracting the average
from each data item. Since there will be about as many items
above average as below average, the resulting list of numbers
will have about as many positive values as negative values.
(In fact this list of deviations-from-average must itself average to zero!)
Square each deviation, and proceed to find the average of the
squared-deviations. However, in finding the average squared-deviation,
divide by N-1 rather than N. The result is the
variance; take its square root to get the standard deviation.
). The standard deviation is simply
the square root of the variance, so lets start by describing
the variance. To obtain the variance start by subtracting the average
from each data item. Since there will be about as many items
above average as below average, the resulting list of numbers
will have about as many positive values as negative values.
(In fact this list of deviations-from-average must itself average to zero!)
Square each deviation, and proceed to find the average of the
squared-deviations. However, in finding the average squared-deviation,
divide by N-1 rather than N. The result is the
variance; take its square root to get the standard deviation.
variance = ( (X01-Xavg)2 +
(X02-Xavg)2 +
(X03-Xavg)2 + ··· +
(X10-Xavg)2 )/9
For data that is "normally distributed" we expect that about
68.3% of the data will be within 1 standard deviation of the mean
(i.e., in the range Xavg ±  ).
In general there is a relationship between the fraction of the
included data and the deviation from the mean in terms
of standard deviations.
).
In general there is a relationship between the fraction of the
included data and the deviation from the mean in terms
of standard deviations.
Fraction Number of Standard
of Data Deviations from Mean
50.0% .674
68.3 1.000
90.0 1.645
95.0 1.960
95.4 2.000
98.0 2.326
99.0 2.576
99.7 3.000
Thus we should expect that 95% of the data would be within 1.96
standard deviations of the mean
(i.e., in the range Xavg ± 1.96  ).
This is called a 95% confidence interval for the sample.
).
This is called a 95% confidence interval for the sample.
The average deviation or mean absolute deviation
is calculated in a similar manner as standard deviation, except here
you subtract the median from each data item producing a list
of deviations from the median. Instead of squaring each deviation,
you take the absolute value of each deviation. Finally you average in the usual
way: using N not N-1.
average deviation = ( |X01-Xmed | +
|X02-Xmed | +
|X03-Xmed | + ··· +
|X10-Xmed | )/10
If the data is "normally distributed" there is a definite relationship
between the average deviation and the standard deviation:
average deviation = 0.80 × standard deviation;
where 0.80 = (2/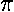 )½.
)½.
Five-Number Summary
The median, you recall, is in the middle of the sorted data.
In a similar way we can define the first quartile to be
1/4 of the way through the sorted data, and
the third quartile to be
3/4 of the way through the sorted data.
(The preferred name for the second quartile is the median, so
that's what we'll call it.) The range between the
first and third quartiles includes half of the data. The size
of the range (i.e., the difference between the third quartile and
the first quartile) is another measurement of variability
called the interquartile range or IQR. For normally
distributed data:
IQR = 1.35 × 
The five-number summary of the data consists of the
minimum data point, the first quartile, the median, the third
quartile, and the maximum data point. Thus these five numbers display
the full range of variation (from minimum to maximum), the
common range of variation (from first to third quartile),
and a typical value (the median).
Standard Deviation of the Estimated Means
The above procedure describes how to define
a "typical" leaf using 10 sample leaves. Clearly if another
group uses the same procedure on its own sample of 10 leaves,
it is unlikely to come up with exactly the same value for
a "typical" leaf. How much variation is there in the estimates of
"typical" described above? Clearly if we expand the sample beyond 10
(to 100, or 1000, ...) we would expect to come closer to the
actual "typical" leaf (i.e., that determined by looking at all the
leaves in the world). Thus the larger the sample you average over, the smaller
is your expected deviation from the exact result. But how much variation
should you expect in a calculated average leaf? The standard
deviation expected in a calculated average is:
 /N1/2
/N1/2
Thus the deviations
expected equal the standard deviation of the length of leaves if you "average" over
just one leaf, and
decrease as the square root of N as N increases. Thus one
can expect to get quite close to the exact mean if the sample size N gets very big.
"Normal" and other Distributions
Many pages have been written by others on this topic. To be brief,
a common assumption of statistics-users is that data is "normally"
distributed. Occasionally the folks making this assumption know
what it means and even test to see if it's a valid assumption. I'm
going to leave you in the dark (like many statistics-users) about
what this assumption means and how you test it. There are several good
courses and books that would include these topics. I will give you two
(not very helpful) hints.
- (Bad News) Many things in nature are not "normally"
distributed. (Good News) Much of what is not "normally" distributed in biology would be
"normally" distributed if you took the logarithm of each data item.
Thus there is a button on the descriptive statistics calculation page
to do this conversion for you. The result is that the geometric
mean is calculated for you and a different kind of standard deviation
is produced.
With the usual standard deviation you add or subtract the standard deviation from the mean
in order to test for fractions of included data; with the log
standard deviation, you multiply or divide. Thus you would expect
68.3% of your data to be between Xgeo×
 and Xgeo÷
and Xgeo÷  ; 95.4% of your data
would be between Xgeo×
; 95.4% of your data
would be between Xgeo×  2
and Xgeo÷
2
and Xgeo÷  2
2
- (Bad News) Much of what's in books about statistics has to do
with "normally" distributed data. Statistics that provide useful
information even if applied to not-"normally" distributed data are
call robust statistics. Median and average deviation are
considered robust statistics. (Good News) The program always
calculates them for you.
There is one additional distribution you should know a bit about:
the Poisson distribution. The Poisson distribution particularly applies
to counts of things, like the number of maple trees per acre or the
number of radioactive decays in an hour. The main upshot is that with things
distributed according to the Poisson distribution, the standard deviation of the
count can be estimated as the square root of the count. Thus if in a particular
experiment you detected 1000 radioactive decays, a full repeat of that experiment
might yield 1030 or 970 or 1037 or 998... The standard deviation of the counts in the
repeated experiments should be close to the square root of 1000 (31.6). Thus
if you don't have the time to do lots of full repeats, the range of
variation you would experience can still be estimated.
 ). The standard deviation is simply
the square root of the variance, so lets start by describing
the variance. To obtain the variance start by subtracting the average
from each data item. Since there will be about as many items
above average as below average, the resulting list of numbers
will have about as many positive values as negative values.
(In fact this list of deviations-from-average must itself average to zero!)
Square each deviation, and proceed to find the average of the
squared-deviations. However, in finding the average squared-deviation,
divide by N-1 rather than N. The result is the
variance; take its square root to get the standard deviation.
). The standard deviation is simply
the square root of the variance, so lets start by describing
the variance. To obtain the variance start by subtracting the average
from each data item. Since there will be about as many items
above average as below average, the resulting list of numbers
will have about as many positive values as negative values.
(In fact this list of deviations-from-average must itself average to zero!)
Square each deviation, and proceed to find the average of the
squared-deviations. However, in finding the average squared-deviation,
divide by N-1 rather than N. The result is the
variance; take its square root to get the standard deviation.
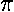 )½.
)½.
