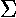Exact Test: Some Details

A random sample of 400 undergraduate students reported their sex (1=male, 2=female) and college (A=business, B=engineering, C=liberal arts, D=nursing, E=pharmacy). The results were sorted into cells where, for example, D2 would be the number of female nursing students (13). The results (with column and row totals) are displayed below.

         A    B    C    D    E  total

    1:  21   16  145    2    6    190
    2:  14    4  175   13    4    210

total:  35   20  320   15   10    400

The individual cell counts are denoted as a matrix: x_ij. x₂₄ would denote the number of female nursing students. The first index i ranges over the rows. The total number of rows is denoted by r ; in our example r=2. The second index j ranges over the columns. The total number of columns is denoted by c; in our example c=5.

The X² test (but not the exact test) makes use of an "expected" contingency table. Whereas the actual contingency table cells must be integers, the expected contingency table cells are real numbers:

e_ij = ( r_i / N ) · ( c_j )

where r_i is the total of the i^th row, c_j is the total of the j^th column, and N is the grand total of the table. For example:

r₂=x₂₁+x₂₂+ x₂₃+ ··· +x_2c

where c (N.B.: c without a subscript) is the total number of columns. In our example r₂=210.

Similarly we can define column totals:

c₄=x₁₄+x₂₄+ x₃₄+ ··· +x_r4

In our example c₄=15, and the sum includes just two terms (since r=2).

In our example the expect table is:

        A      B      C      D      E

1    16.6    9.5    152    7.1    4.8    
2    18.4   10.5    168    7.9    5.8    

X² is then defined by:

X² = 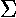(x_ij - e_ij)²/e_ij

As described on another page if any e_ij are "small" (say less than 5), we have problems and another approach may be needed. (In this example, we have one expected cell smaller than 5. However, by the Cochran conditions, this table can still be analyzed with X².)

One option is the exact method. In the exact method, we view the particular contingency table x_ij as embedded in a universe of similar tables that have the same outcome probabilities as our table (i.e., have the same row totals) and the same distribution of treatments (i.e., have the same column totals). The probability of each table in this universe can be calculated:

p = (r₁! · r₂! ··· r_r!) × (c₁! · c₂! ··· c_c!) / (x₁₁! · x₁₂! ··· x_rc! × N!)

We then seek the sum of the probabilities of every table that is as unusual as the given table. That is, p for the exact test is the sum of all table probabilities less than or equal to the given table's probability. If the total of such probabilities is "small" we deem it unlikely to have observed such a table and hence reject the null hypothesis of independence.

The main problem of applying the exact test is that for moderately sized tables, the number of table probabilities to be enumerated can easily reach the billions. As stated before, Mehta and Patel [J. Am. Stat. Assoc. 78 (1983) 427-434] found a clever recursive method of summing the probability in the required tables, but even so large tables can exhaust a modern computer. SO, if X² is allowed, use it!