z-Test

Experiment 1 produces result x1 with uncertainty σ1.

Experiment 2 produces result x2 with uncertainty σ2.

Are the results so different that they cannot be the same value? P reports the two-tailed probability of by chance getting such (or more) divergent results. If P is small (say <.05) reject the null hypothesis that they are within random variation. (Remark: while statisticians may be excited by |z|>2, experienced physicists rarely get excited until |z|>3.)

x1=     σ1=

x2=     σ2=

Details: The null hypothesis is that x1-x2 is normally distributed with mean 0 and variance σ12+σ22. Typically x1-x2 is not zero, and we find the probability that it could be that or more divergent, e.g., if |z|=2 we would calculate the area P shaded below:

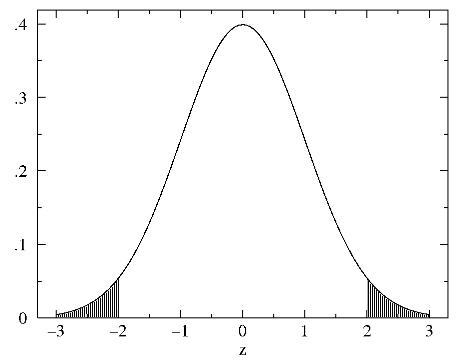
In general P can be plotted as a function of |z|

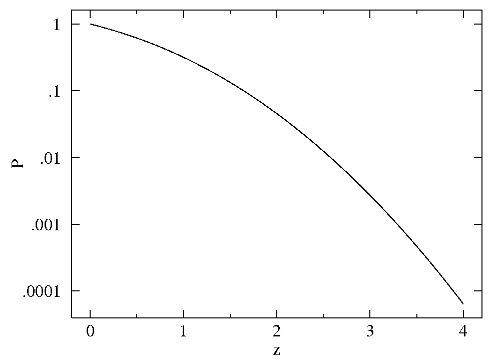
"critical" (i.e., commonly used) values 

|z|     P
0.674   0.5
1       0.317
1.645   0.1
1.960   0.05
2       0.0455
2.576   0.01
2.807   0.005
3       0.00270
3.291   0.001
3.481   0.0005
3.891   0.0001
4       0.0000633