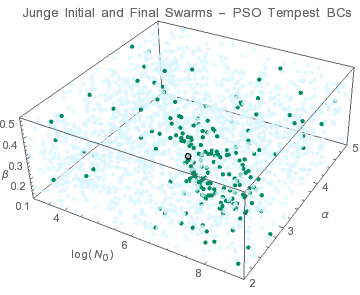
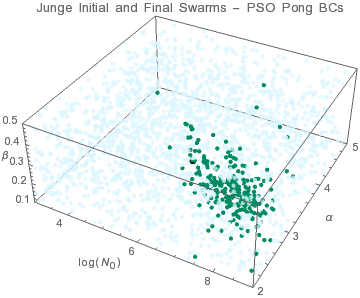
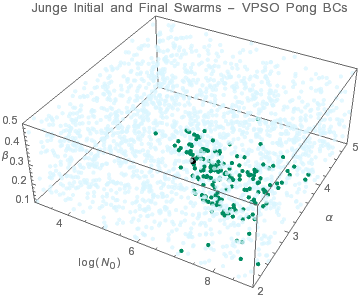
● target solution ● initial swarms ● final swarms
Synthetic data sets are used to test the degree of swarm convergence for the following algorithms:
Average parameter values with uncertainties appearing in the results tables below using the method described by DuPaul (AJUR, submitted 02/14/2017) to reduce the set of ten parameter values based on the reduced chi-squared for aerosol optical depths calculated from the size distributions.



● target solution ● initial swarms ● final swarms
| Solution | N0×β (cm–3) | α |
|---|---|---|
| Target | 7.5×105 | 3 |
| PSO - tempest | (7.499919±0.4)×105 | 3 |
| PSO - pong | (7.499922±0.5)×105 | 3 |
| VPSO - pong | (7.499915±0.6)×105 | 3 |
Since N0 and β are not independent, the swarm convergence appears to be weak with many individuals unable to converge before the performance criteria are met. However, the factor N0×β is what is important for this distribution and all algorithms yield the same result.
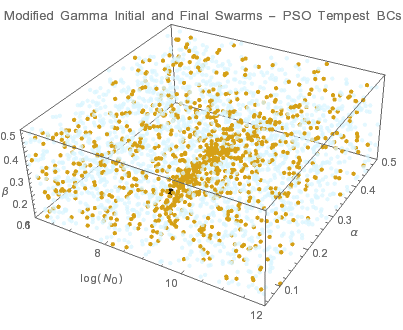
● target solution ● initial swarms ● final swarms
| Solution | N0 (cm–(3+β)) | α (μm–1) | β |
|---|---|---|---|
| Target | 2.5×109 | 0.1 | 0.35 |
| PSO - tempest | (2.6±0.8)×109 | 0.097±0.007 | 0.33±0.04 |
| PSO - pong | (2.5±0.7)×109 | 0.098±0.005 | 0.34±0.03 |
| VPSO - pong | (4.0±0.7)×109 | 0.100±0.004 | 0.40±0.02 |
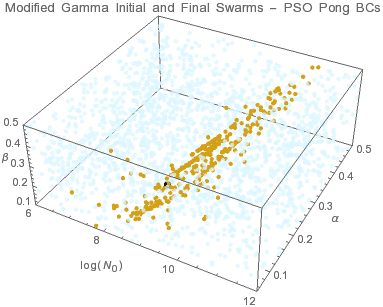
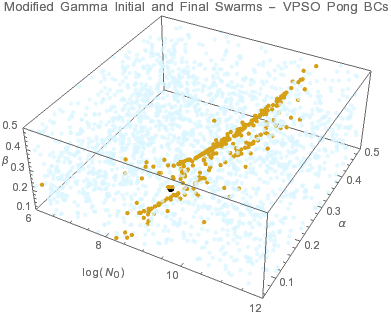
The peak of this modified gamma distribution occurs at rp = β/α. β affects the small r behavior while α affects rp and hence the large r behavior. In a log-log plot of nG(r), β is the slope for r < 1 while the drop of for r > rp is affected by both α and β. The individuals tend to converge to a surface within the solution domain. This means that there are multiple size distributions that can yield the same set of aerosol optical depths within instrument accuracy. The possibility of having multiple valid size distributions is reflected in the uncertainties associated with the distribution parameters. The results indicate that PSO-pong is the most accurate algorithm.
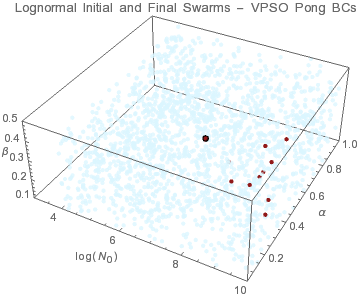
● target solution ● initial swarms ● final swarms
| Solution | N0 (cm–2) | α (μm) | β | rmode (μm) | rmean (μm) |
|---|---|---|---|---|---|
| Target | 1.0×107 | 0.500 | 0.307 | 0.455 | 0.524 |
| PSO - tempest | 1.0×107 | 0.500 | 0.307 | 0.455 | 0.524 |
| PSO - pong | 1.0×107 | 0.500 | 0.307 | 0.455 | 0.524 |
| VPSO - pong | 1.0×107 | 0.500 | 0.307 | 0.455 | 0.524 |
All algorithms are equally good at resolving the target solution. Individuals tend to converge to a point within the solution domain, with a few straggling behind unable to converge before the performance criteria are met.
Aitken Mode
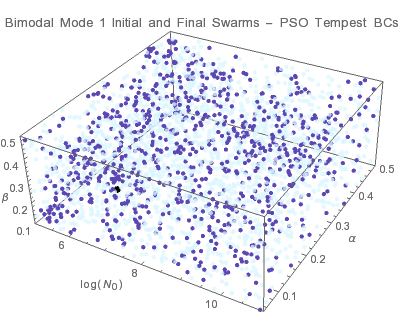
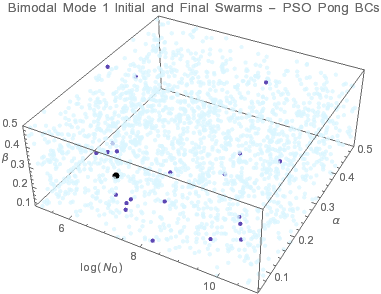
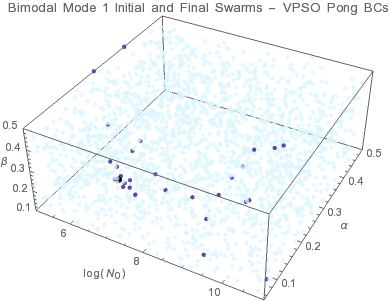
● target solution ● initial swarms ● final swarms
Accumulation Mode
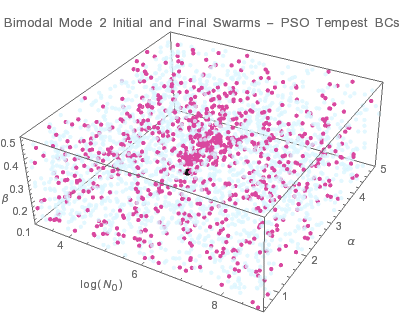
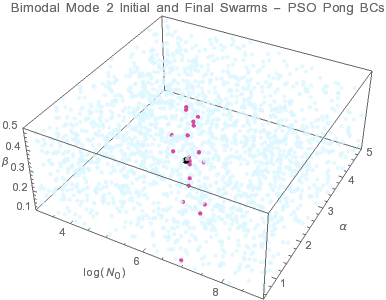
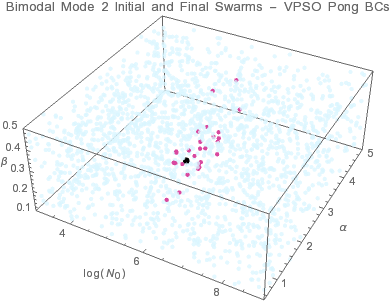
● target solution ● initial swarms ● final swarms
| Solution | N0 (cm–2) | α0 (μm) | β0 | N1 (cm–2) | α1 (μm) | β1 | r0,mode (μm) | r0,mean (μm) | r1,mode (μm) | r1,mean (μm) |
|---|---|---|---|---|---|---|---|---|---|---|
| Target | 1.0×107 | 0.100 | 0.307 | 1.0×106 | 2.00 | 0.307 | 0.091 | 0.105 | 1.820 | 2.097 |
| PSO - tempest | (2.1±1.1)×107 | 0.102±0.017 | 0.28±0.04 | (8.1±0.4)×106 | 2.28±0.09 | 0.28±0.03 | 0.095±0.016 | 0.107±0.018 | 2.10±0.09 | 2.37±0.10 |
| PSO - pong | (1.0±0.5)×107 | 0.118±0.011 | 0.27±0.05 | (1.15±0.27)×106 | 1.94±0.24 | 0.32±0.05 | 0.110±0.011 | 0.122±0.012 | 1.75±0.23 | 2.05±0.26 |
| VPSO - pong | (2.4±1.1)×107 | 0.118±0.027 | 0.30±0.05 | (1.08±0.22)×106 | 2.12±0.25 | 0.29±0.05 | 0.107±0.025 | 0.123±0.028 | 1.95±0.23 | 2.21±0.26 |
Individuals tend to converge to a point within the solution domain. Trade-offs between the Aitken mode and accumulation mode parameters lead to multiple valid size distributions as indicated by the uncertainties in the size distribution parameters. The results indicate that PSO-pong is the best overal algorithm when considering both accuracy and precision.