Good lab skills are the key to success in science. Almost certainly your first job in science will not resemble an exam: with lots of pencil pushing on made-up problems; rather it will most resemble lab: where you use equipment to collect data on real ---less than perfect--- objects.
There is no such thing as a dumb question. Questions during lecture do not "interrupt" the lecture, rather they indicate your interests or misunderstandings. I'd much rather clear up a misunderstanding or discuss a topic of interest than continue a dull lecture.
Remember: you are almost never alone in your interests, your misunderstandings, or your problems. Please help your classmates by asking any question vaguely related to physics. If you don't want to ask your question during class, that's fine too: I can be found almost any time in my office (PEngel 111) or the nearby labs. Drop in any time!
This course covers the discoveries of Isaac Newton (1642-1727) and the founders of thermodynamics (e.g., Sadi Carnot (1796-1832), James Joule (1818-1889), William Thomson, 1st Baron Kelvin, (1824-1907), James Clerk Maxwell (1831-1879), Willard Gibbs (1839-1903), and Ludwig Boltzmann (1844-1906)) which are the foundation of the science and technology that transformed the animal powered world of Newton into the mechanized world of today. The basis for Newton's discoveries was that the universe follows mathematical laws, so improvements to technology can be calculated rather than found by trial and error. This idea of a mathematical universe is ancient (e.g., often attributed to Pythagoras (ca. 585-497 B.C.)) so one might wonder why it didn't happen much earlier: Why, for example, didn't Archimedes (287-212 B.C.), often called the Newton of the ancient world, "scoop" Newton and discover the mathematical rules that govern the universe? Imagine: Joseph an auto mechanic rather than a carpenter.
The key discovery that Newton made (and that Archimedes "almost" made)
was the differential equation. Differential equations are probably
beyond your current mathematical studies
(MATH 337: Differential Equations) but the basic idea is
simple. When you think
of an equation you may be thinking of something
like:
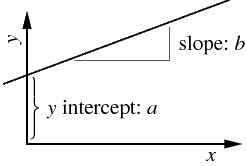
y = a + bx

Equations like this are particularly nice because if
you know the numerical values of all the things on the right
hand side (a,b,x) you can calculate the value of the
thing on the left hand side (y). In some sense such an
equation gives the relationship between x and y completely and immediately.
For example, in the case of the ideal gas law: PV=nRT, if you know
the numerical value of any four of the quantities you can calculate the fifth.
What Newton discovered1was that the fundamental laws of
nature are not equations like the above. Instead of
giving us the the whole story in one package (an equation)
nature's rules focus on change, reporting how things
change with time or position. For example,
one could equally well describe a straight line by saying it has
unchanging slope which translates to the differential
equation:
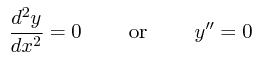
Thus a differential equation is an equation that includes
derivatives, i.e., changes. (A philosophical question:
Why are the universe's laws differential equations
rather than some other sort of magic or mathematics?)
A mathematics course in differential equations teaches you how to
go from a differential equation, which tells you how things
change, to an equation, which gives you the complete story.
Science courses then explain which differential equations are used by nature.
Remark: mathematics usually uses the generic variable names x
and y, whereas in science we're most commonly concerned with
how things change in time. Thus the thing that
in your math class is labeled x will most often in your
science classes be labeled t. In this physics class, we'll
often be concerned with the position of objects which we'll often label
x. Thus to translate from your math class to your physics
class: x → t and y → x . Thus a typical
physics equation is:
x = x0 + v0t + ½a t2
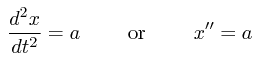
A major stumbling block should now be evident. The universe speaks in the language of differential equations and most of you will never take the intro course in that language. Thus the process of translating from the fundamental laws of nature (like Newton's three laws) to the immediately usable equations will sometimes seem mystifying, awkward and uninteresting. One might make the mistake of trying to "learn physics" by memorizing dozens of equations rather than understanding the general equations that apply to any possible situation.
This course will focus on applying Newton's laws of motion to three situations: (A) motion with a constant applied force, (B) motion in a circle at constant speed, and (C) oscillatory motion. Clearly these three situations are a small subset of real life motions. Please realize that Newton's laws explain equally easily all real-life motions, but we need additional mathematical tools to apply them to more complicated situations.
Implicit in the concept "motion" is the idea of change. Nevertheless, physics has discovered quantities that stay constant even as most every common-sense quantity associated with a motion varies. These quantities that stay constant --- called conserved quantities --- provide simple ways of understanding motions. In this course we will be particularly interested in the conservation of (A) energy, (B) linear momentum, and (C) angular momentum. (An analogy: when a log burns initially we have wood and oxygen and finally we have hot gases and ash. Everything seems changed. Nevertheless you've learned that the number of carbon atoms stayed constant during the reaction. In chemistry the conservation of atoms during chemical reactions is a great unifying principle.)
Thermodynamics rests on four "laws", which in turn rest on the mechanics of large numbers of particles. While Newtonian mechanics is adequate for much of thermodynamics, various puzzles ushered in "quantum mechanics" in the early decades of the last century.
There are a couple of aspects of this course that make it particularly difficult. First, things do not work the way common sense tells you: often you'll find your intuition misleading you. You step on the car's accelerator and you're pushed back in the seat; common-sense says the cause is "inertia". You round a corner and the books that were sitting on the car seat are thrown to the side; common sense says the cause is "centrifugal force". In this course you will learn that "centrifugal force" and "inertia" play no role in the true explanation of motion. I know it is impossible for you to throw out the understanding of how the world works that you've developed over your lifetime and substitute the correct but weird and abstract laws of motion discovered by Newton. 42 hours of instruction can not overcome a lifetime of experience. I do hope that in a few artificial examples you'll know --- but perhaps not truly believe --- how the laws of motion apply. Think about it: you've spent a lifetime observing the universe and have come to wrong conclusions about how it works. (But those wrong conclusions are still useful to predict the behavior of your car. A follower of Bokononism would call your conclusions --- and Newton's --- foma2.) You might now conclude that the human mind was not built to comprehend the true causes of the universe. But the actual result is far stranger than that. First the famous Einstein quote: "The most incomprehensible thing about the universe is that it is comprehensible." Now the true causes of the universe are not yet totally known, and it is quite possible that when/if discovered they will be understandable only to a few thousand physicists. What we already know is that the road to comprehending the universe has been a series of steps. Common sense ideas of how the world works were written down by Aristotle (384-322 B.C.) replacing unwritten ideas that served mankind for the previous million years. Aristotle's physics was good enough to build cathedrals and catapults and is probably accurate enough for the vast majority of people who do not need understand how a bird flies let alone design an airplane. Newton's "F=ma" is a tremendous leap forward in understanding, explaining 99% of everyday experience, but it is not the last word. Electrodynamics, statistical mechanics, quantum mechanics, relativity, relativistic quantum field theory..., each step forward has been based on the previous steps, in such a way that each advancement seems impossible without the previous (incorrect) steps. (I cannot imagine how quantum mechanics could have been discovered unless Newtonian mechanics had been discovered first.) Thus our growing comprehension as to how the world works has been structured like learning from a good user's manual: the most useful stuff comes first and then each further refinement is explained. While the universe might not be comprehensible in one gulp, it seems there is a step-by-step approach you can follow to understand it. But expect "common sense" to fight every step forward.
Second, since the universe follows mathematical laws, in order to understand the universe you must be able to do mathematics. In this course we will use most of the mathematics you've learned over your lifetime: arithmetic, geometry, trigonometry, algebra, and a touch of calculus. Trying to recall the mathematics you learned a couple of years ago and apply it in new situations is challenging. The best tonics for this problem are to ask lots of questions and work lots of problems. (Yes, work problems that are not assigned.) In addition carefully study the "Problem Solving Tactics" sprinkled throughout our textbook and read the advice recorded on the class web page.
One final point: it is important to remember that the subject of our study is not the book; it is nature. This course will serve you best if you try to apply what you are learning to the world you experience everyday.
| Day | Date | Text | Topics | Exams | Labs (Days: 1-3) | |
| 1/2 | R | Aug 30 | 1.1-1.9 | Measurements, Trig | Uncertainties | |
| 1/4 | M | Sep 3 | 2.1-2.4 | Position, Velocity, Acceleration | ||
| 1/6 | W | Sep 5 | 2.4-2.6 | Constant Acceleration Problems | ||
| 2/2 | F | Sep 7 | 3.1-3.3 | Vectors | QUIZ 1 | Data Analysis |
| 2/4 | T | Sep 11 | 3.4-3.5 | Two Dimensional Motion | ||
| 2/6 | R | Sep 13 | 4.1-4.4 | Newton's Laws | QUIZ 2 | |
| 3/2 | M | Sep 17 | 4.5 | Applications | Free Fall | |
| 3/4 | W | Sep 19 | 4.6 | Friction | ||
| 3/6 | F | Sep 21 | 1.1-4.6 | Review | QUIZ 3 | |
| 4/2 | T | Sep 25 | 1.1-4.6 | Math & Motion | Exam 1 | Projectile Motion |
| 4/4 | R | Sep 27 | 5.1-5.3 | K.E., Work & P.E. | ||
| 4/6 | M | Oct 1 | 5.4-5.7 | Non-Constant Forces: Springs, etc. | ||
| 5/2 | W | Oct 3 | 6.1-6.2 | Impulse & Momentum | QUIZ 4 | Kinetic Friction |
| 5/4 | T | Oct 9 | 6.3-6.5 | Collisions | ||
| 5/6 | R | Oct 11 | 7.1-7.4 | Centripetal Acceleration | QUIZ 5 | |
| 6/2 | M | Oct 15 | 7.4-7.6 | Gravity & Orbits | Ballistic Pendulum | |
| 6/4 | W | Oct 17 | 8.1-8.4 | Torque & Equilibrium | ||
| 6/6 | F | Oct 19 | 8.5-8.7 | Rotational Dynamics | QUIZ 6 | |
| 7/2 | T | Oct 23 | 5.1-8.7 | Review | Rotational Dynamics | |
| 7/4 | R | Oct 25 | 5.1-8.7 | Energy & Rotation | Exam 2 | |
| 7/6 | M | Oct 29 | 9.1-9.6 | Pressure & Buoyant Force | ||
| 8/2 | W | Oct 31 | 9.6-9.8 | Bernoulli's Equation | ||
| 8/4 | F | Nov 2 | 9.8-9.10 | Fluids in Practice | QUIZ 7 | |
| 8/6 | T | Nov 6 | 10.1-10.4 | Temperature | ||
| 9/2 | R | Nov 8 | 10.4-10.5 | Ideal Gas, Kinetic Theory | Archimedes' Principle | |
| 9/4 | M | Nov 12 | 11.1-11.4 | Calorimetry: Specific & Latent Heats | ||
| 9/6 | W | Nov 14 | 11.4-11.6 | Energy Transfer | QUIZ 8 | |
| 10/2 | F | Nov 16 | 12.1-12.3 | First Law of Thermodynamics & Work | ||
| 10/4 | T | Nov 20 | 12.3-12.6 | Entropy & Second Law | ||
| Thanksgiving Break: Wednesday-Friday | ||||||
| 10/6 | T | Nov 27 | 9.1-12.6 | Review | QUIZ 9 | |
| 11/2 | R | Nov 29 | 9.1-12.6 | Thermodynamics & Fluids | Exam 3 | Gas Behavior |
| 11/4 | M | Dec 3 | 13.1-13.4 | Oscillations: Amplitude, Frequency | ||
| 11/6 | W | Dec 5 | 13.4-13.6 | Examples | ||
| 12/2 | F | Dec 7 | 13.71-13.9 | Waves | QUIZ 10 | Lab Practical Exam |
| 12/4 | T | Dec 11 | 13.9-13.11 | Interference & Reflection | ||
| 12/6 | R | Dec 13 | 1-13 | Review | QUIZ 11 | |
| M | Dec 17 | 1-13 | Everything! | Final Exam | ||