While the delta function lattice provides a simplest model a lattice (and hence of band structure), it would be nice to have a bit more complexity in our model: after all, solid state physics has had a singular effect on technology and a core concept in sold state is the band structure of crystals. Unfortunately, the next step up turns out to a rather sizable leap.
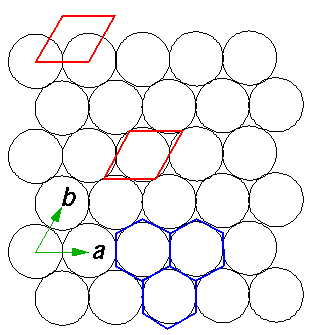
We begin with about the simplest non-trivial crystal: 2D hexangular closest packed. We imagine a 2D array of range-limited circularly-symmetric attractive potentials:

The black circles represent the lattice of attractive potentials. We'll assume that in the limited space between the circles, the potential is zero. Our aim is to provide a toy model for the motions of the valance electrons through a crystal of, say, Silicon. The attraction of the valence electrons to the Si ion (nucleus + core electrons) is modeled by our array of attractive potentials. Obviously real crystals are 3d arrays of atoms, we've gone down to just 2d for simplicity. (Nevertheless, you should know that the motions of electrons through real 2d crystals --so called 2d electron gases: 2DEG-- is a topic of great experimental and theoretical interest.)
Like any lattice, this crystal can be thought of as one cell simply repeated all over the plane. The repeat vectors a and b show the periods of the lattice. We could say that a and b generate the lattice. We can think of the lattice of a honey-comb of (blue) hexagons or a slanted tiling of (red) rhombuses: either will cover the plane if repeated as directed by a and b. Since the rhombus is easier to grid (see below) we will make frequent use of it. Since the hexagons display the symmetry of the lattice better and are a more "centered" tiling we'll also make use of them.
The symmetries of the lattice turns out to be quite interesting. Notice that 60° rotations about the centers of the hexagons leave the entire lattice invariant. The sides of the top rhombus (or the diagonals of the centered rhombus) could be extended to be symmetric planes of reflection. The collection of symmetry operations (including basic translation) can be used to classify lattices. The name Group Theory must be mentioned even though I don't have time to explain it here.
We will assume that inside each circle the potential is quadratic. Thus if we move along the the short diagonal of the centered rhombus, the potential would look like:
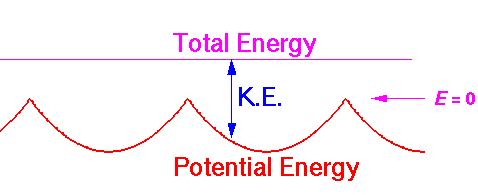
In this case the particle's total energy is greater than zero; the particle has no turning points it is free to roam the entire plane. The particle's trajectory through the plane will depend critically on the initial position and velocity, as the particle is continually knocked around by the potential wells.
Along the long diagonal of the centered rhombus we have long sections "outside" of the potential wells:
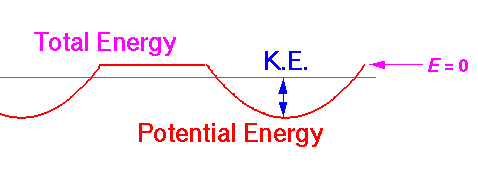
In this case I have displayed a particle with less than zero energy. It is confined to one well; classically the particle would rattle around inside the well and never tunnel through the region where it would have to have negative kinetic energy.