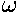,
the argument of periastron. The angle between the ascending node
and the direction towards the north celestial pole (NCP) is the
position angle of the ascending node and is denoted by 
.
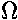We use three angles to describe the orientation of star orbits.
If we view an orbit "face on", i.e., with the plane of the orbit perpendictular
to our line of sight, we say that it has inclination zero.
In general, the angle between the orbital plane and the plane perpendictular
to our line of sight, is the inclination and is denoted by i.
If the orbit has a non-zero inclination, then the plane that includes
the orbit-focus and is perpendictular to our line of sight intersects
the plane of the orbit in a line called the line of nodes. The
orbit intersects the line of nodes at two points called nodes.
At one node (called the ascending node) the orbiting star would be moving
away from the Earth; this is the ascending node. At the other node the orbiting
star would be approaching the Earth; this is the descending node. The line to
the ascending node is particularly important in describing the orbit. The angle
in the plane of the orbit from the asceding node to "perihelion" (the point in the
orbit at which the stars are closest together) is ,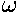
the argument of periastron. The angle between the ascending node
and the direction towards the north celestial pole (NCP) is the
position angle of the ascending node and is denoted by .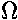
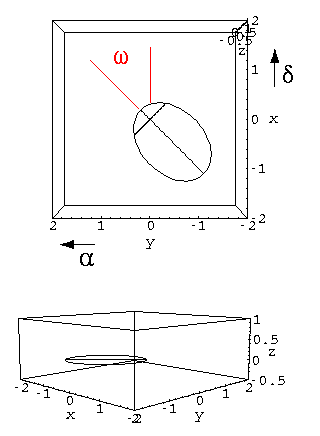
We can imagine starting with an orbit in a standard position and determining what rotations are needed to move it into its actual orientation. In our standard position, Earth sits far out the positive z axis. The x+ axis points towards the NCP and the y+ axis points in the direction of increasing right ascenscion. Initially the orbit is orientated with the major axis along the x axis and with "perihelion" on the positive x axis. Then we perform the following rotations to orient the orbit in space:
| 
| 
|
| Rotate the orbit an angle from the direction of increasing
declination (i.e., direction towards the NCP). This line will soon include an ascending node.
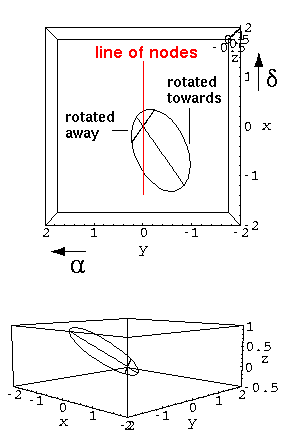
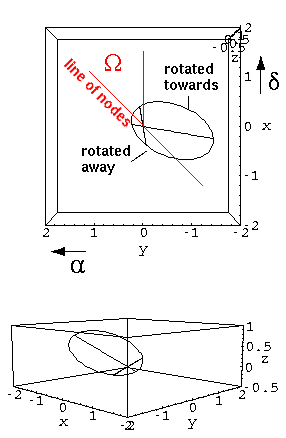
| Incline the orbit an angle i, creating an ascending node due north of the orbit focus. This rotation 0° <= i <= 180° is performed along the negative x axis. | Rotate the line of nodes an angle 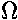from the direction of increasing
declination.
|
QuickTime movie of orbit Orientation (0.5 MB)
Note that "nearby" orbit orientations can have quite different coordinate
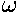(, i,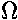) descriptions.
For example, if we consider an orbit just like that in the standard position,
but with "perihelion" pushed back a degree, see that then the line of nodes
will be on the y axis. "Perihelion" will be 90° from the line of
nodes and the ascending node will be -90° from north. Thus:
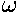(, i,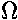) = (90°, 1°,-90°)
In cases of small inclination the sum of 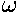and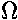
may be more accurately known than eithe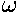r or .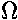
In such cases it is useful to report:
= +
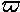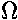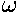
The orbital ellipse we see the stars following in the sky is a projection
of the actual orbital ellipse. Can we determine the actual orbit from the
apparent orbit we measure in the sky? Five parameters determine an orbit:
a semimajor axis and e eccentricity in addition to
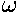(,i,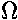). (To determine
the position at a particular time we would also need the orbital period P
and some sort of initial point, say the time T when the star was at
"perihelion".) From the apparent orbit we can determine 5 parameters:
the eccentricity and semimajor axis of the apparent orbit, the position angle of the apparent
major axis, and the (
, 
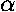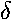) offset between
the apparent ellipse's focus and the projected location of the actual ellipse's focus.
From 5 measured parameters we can have hope of determining the 5 independent parameters
that describe the true orbit, and in fact this hope is largely acheived. As it turns out
the one thing we can't distinguish in projection the ascending node from the
desending node. In essence an orbit with inclination -i projects exactly
the same as one with +i.