Quantum Mechanics Examples

5½ Examples in Quantum Mechanics

The new theories, if one looks apart from their mathematical setting, are built up from physical concepts which cannot be explained in terms of things previously known to the student, which cannot even be explained adequately in words at all. Like the fundamental concepts (e.g., proximity, identity) which every one must learn on his arrival into the world, the newer concepts of physics can be mastered only by long familiarity with their properties and uses.
P.A.M. Dirac (1930) Preface The Principles of Quantum Mechanics

We have always had a great deal of difficulty understanding the world view that quantum mechanics represents. At least I do, because I'm an old enough man that I haven't got to the point that this stuff is obvious to me. Okay, I still get nervous with it... You know how it is, every new idea, it takes a generation or two until it becomes obvious that there's no real problem... I cannot define the real problem, therefore I suspect there's no real problem, but I'm not sure there's no real problem.
R. P. Feynman as quoted in Genius (1992)

Preface

As the above quotations suggest, quantum mechanics is difficult, or perhaps impossible to understand (Steven Weinberg: "no one fully understands" [quantum mechanics]). Nevertheless, quantum mechanics is used on a daily basis by thousands of physicists, chemists and engineers. (E.g., Nobel prize winning chemist Linus Pauling: "There is no part of chemistry that does not depend, in its fundamental theory, upon quantum principles.") The ability to use quantum mechanics depends in part on mechanical mathematical skills ("doing the algebra", now made much easier with programs such as Mathematica) but more importantly on "physical intuition". Unfortunately our bedrock intuition -- based on classical mechanics -- is often at odds with quantum mechanics. This does not mean you must discard your hard-won classical intuition, rather you should treasure those parts that survive into quantum mechanics. These pages try find common ground between Newton's explanations and Schrödinger's explanations. In addition because of the revolution in computer algebra (e.g., Mathematica), these pages try to formulate problems in ways that allow easy translation into Mathematica code. Often simple practices (like the use of dimensionless variables) make understanding easier for both the computer and the human. Finally I should note that these pages are aimed at folks who want to do quantum mechanics. Like Dirac, I believe that the apprentice quantum mechanic gains facility by practice. I hope that you will do the examples, not just read the examples. A set of problems at the end of each "chapter" provide extentions of the examples. Feel free to write me if you have questions or comments!

Introduction: Classical Mechanics First!

Usually books on quantum mechanics start with quantum mechanics. Instead I start with a brief review of examples in classical mechanics. Note that all of the below descriptions of classical motion report how the particle's position and velocity change in time. Quantum descriptions must be quite different because quantum mechanics asserts that a particle does not have a position and a velocity. Instead the particle has, in some sense, simultaneously a range of possible positions and velocities. The particle has some chance of being found here, another chance of being found there, etc. Position is not a property that a particle has any more than a die has the property of the number that comes up. The die actually has is a range of possible outcomes (1-6) with a probability for each outcome (1/6). So too with position, but rather than just having a finite list of possibilities, usually a particle's position will be found within a continuous range of possibilities. Thus we seek the probability density for a particle's position. The aim of quantum mechanics is to calculate this range of possible particle positions and the relative probability of those positions. This sounds nothing like classical mechanics!

In classical mechanics if we say that the particle has a position of 100±1, we mean that the particle has a position in the range: 99-101, we're just not sure where. In quantum mechanics if we say that the particle has a position of 100±1, we mean that the particle is simultaneously all over the range: 99-101. This ability to be "spread out" is not surprising for waves (in fact it would make little sense to say the wave is localized to a region smaller than a wavelength... a wave needs at least a wavelength to "wave"); here we apply this wave property to things like electrons, which are traditionally called "particles".

Almost all standard courses in calculus-based introductory physics describe three examples of motion:

Constant Force F-- e.g., motion of an object falling a few meters near the surface of the Earth (in which case the constant force depends on the particle's mass: F=-mg, resulting in all falling objects having the same (downward) acceleration: g=9.8 m/s²)
a=F/m=-g: acceleration is the result of applying the force; it can be calculated by the force divided by the particle's mass
z(t)=z₀+v₀t+½at²: the height of the object (z) depends on the initial height (z₀), the initial velocity (v₀) and time (t)
v(t)=v₀+at: the velocity changes uniformly in time from its initial value
U(z)=-Fz=mgz: the potential energy has the property that if you take minus the derivative of it w.r.t. position, you get the force. -Fz + constant works; we've set the constant equal to zero.
In the case of the ball falling near the surface of the Earth, the above described motion cannot continue indefinitely as the ball soon encounters the ground. In the case of a perfectly elastic collision with the ground, the ground provides a force to exactly reverse the ball's velocity. It bounces forever between the ground (z=0) and some maximum height (z_max) that depends on its energy.
Spring Force (Hooke's Law) F=-kx -- e.g., a force that always pulls the object back to the equilibrium position (x=0)...if x>0, the force is in the negative x direction, etc.
x(t)=A sin(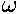t+): the particle oscillates around equilibrium getting as far away as ±A. The period, T (the time it takes to make one complete oscillation), is determined by 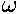(the angular frequency): T=2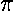/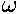. 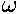is in turn determined by the strength of the spring, k (called the spring constant) and the mass m: 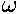²=k/m. Thus a strong spring connected to a light particle will oscillate quickly, i.e., with a short period.
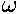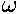v(t)=A cos(t+): the velocity (v) of the particle also oscillates, i.e., sometimes the particles is moving to the right (positive v) sometimes it is moving to the left (negative v). Notice that the particle has is maximum speed (of A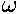) when the cosine term reaches its extremes of ±1. That happens only when sine is zero (because cos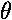²+sin²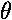=1) and hence the particle is moving through the equilibrium position (x=0). Similarly, the particle is momentarily at rest (v=0) only when the particle is at an extreme position (±A; i.e., if cosine is zero, sine must be ±1).
U(x)=½kx²: the potential energy has the property that if you take minus the derivative of it w.r.t. position, you get the force. ½kx² + constant works; we've set the constant equal to zero.
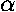Orbital Motion: motion of a particle with a /r² central force applied. In intro physics the topic was the motion of planets under the influence of the Sun's gravitational force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same" as far a physics goes) but quite different distance scales. In addition energy emission by gravitational radiation is totally negligible in the Solar System, whereas energy emission by electromagnetic radiation (light) should be important in an atom.
Planets move in ellipses with the Sun at one focus. Ellipses can be described in terms of their semi-major axis, a, (basically the longest radius) and their eccentricity (basically how squashed the ellipse is: e=0 is a circle, a fully squashed ellipse looks like a line and has e=1).
r=a(1-e²)/(1+e cos()); r_min= a(1-e); r_max=a(1+e)
, the polar angle from closest approach is given the odd name: true anomaly. The timing of the motion (i.e., when the planet or electron has a particular ) is a bit complex. The game is to express the true anomaly () in terms of the eccentric anomaly (u) and then find an expression relating time and the eccentric anomaly. 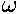For nearly circular orbits it turns out that the true anomaly, the eccentric anomaly, and the mean anomaly (t) are all approximately equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly, the formula relating these two, and the formula relating time and the eccentric anomaly.

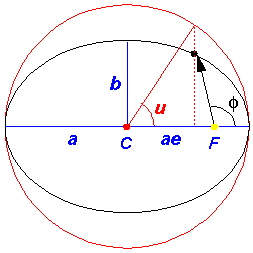
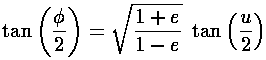
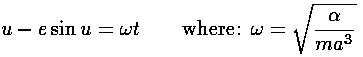
In the above picture, the yellow dot represents the Sun (or a nucleus); it is at a focus (F) of the ellipse. The red parts of the diagram have to do with the geometric construction for the eccentric anomaly which is measured from the center (C) of the ellipse. There is nothing physically at the center of the ellipse, this is all just part of a geometric construction. The blue parts of the diagram relate the semi-major axis (a) and the distance between the ellipse center and the focus (ae). The semi-minor axis, b, can be related to the semi-major axis and the eccentricity:
b = a(1-e²)^½
The black ellipse is the orbit of the particle, i.e., the set of positions the particle will traverse during a period (T=2/).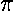
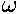The velocity vector is, of course, changing as the position vector is changing. The set of velocities the particle will have during a period is called the hodograph; it's just like an orbit, but for velocity rather than position. The hodograph is surprising: it's just a circle, but the center of the circle is not v=0.

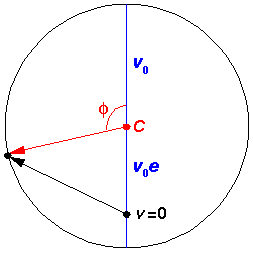
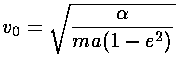
Note that at closest approach to the "Sun" (=0) the speed is a maximum and the velocity points in the y direction, whereas at the far point (=180°) the speed is a minimum and the velocity points in the -y direction. As the eccentricity approaches 1, the maximum speed gets arbitrarily large and the minimum speed approaches zero.
The above figures have been drawn with a rather large eccentricity: e=.707. For eccentricities similar to those of the planets it would be hard to distinguish the elliptical orbit from a circle (although for some planets--like Mars--the position of the Sun would look noticeably "off-center"...because the Sun is at a focus rather than the center).
If the (attractive) radial force is given by: F_r=-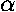/r², the potential energy is U(r)=-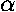/r, so that the minus derivative of U is the force. Notice that just like the spring (which also attracts to the origin), the potential energy is ever smaller as you approach the origin. Unlike the spring, this potential energy is numerically negative (i.e., U(r)<0). That is a result of our choice of additive constant. For the spring we choose the potential to be zero at the origin, forcing the potential to be arbitrarily big as x approaches infinity. For this problem we take the potential energy to be zero as r approaches infinity, so the potential at the origin must be infinitely less, i.e., negative infinity.

Most introductory courses in quantum mechanics start out with problems that are not one of the above classical problems: "square well" potentials also known as particle-in-a-box problems, and delta function potentials.
"Square well" potentials are very odd cases where the potential is constant except for a few steps up or down. Since the force is the minus derivative of the potential, and the potential is flat everywhere you can take its derivative, these problems correspond to cases where the force is zero (i.e., a "free" particle) almost everywhere. The only places where the force is not zero are the points where the potential takes a step up or down. A step up corresponds to a infinitely strong force to the left; a step down corresponds to a infinitely strong force to the right. Again the particle would only feel those infinite forces at the point where the step happens, otherwise the force is zero. In the case of a potential "well" (say, U(x)=0 if |x|<a and U(x)=U₀ if |x|>a) the force is zero except at x=±a. A particle, say starting at the origin and moving in the positive x direction, would move at a constant velocity until it was actually at x=a. At that point the particle would experience an infinite force pushing it to the left. If the particle is moving fast enough, the force only slows it down, and the particle moves on to the force-free region x>a now moving at a constant but reduced speed. If the particle is not moving fast enough, the force is able to reverse its motion and the particle heads back towards the origin with its velocity reversed and at an undiminished speed. It will soon hit x=-a, where it will again "bounce"...the particle is trapped between x=-a and x=a. In the "infinite square well" version of this problem, the jump in potential energy is itself infinite; no particle is able to "punch" through the forces at x=±a; all particles are forced to forever bounce between x=-a and x=a.
½ "Delta function" potentials are even odder. Like square wells, the potential is almost everywhere a constant (0) and so, almost everywhere, there are no forces acting on the particle. At a single point the potential undergoes a tremendous jump. So high is the jump that there is a finite area under this single point. With an attractive delta function potential, a particle is attracted to the potential only when it is actually on top of the single point of attraction; at all other points the force is zero on the particle.
Electrons in a lattice: While it is unsurprising that the exotic in physics (e.g., particle physics; cosmology) gets disproportional press, there is probably no single aspect of physics that has influenced the world as much as the physics of everyday solids. The most typical problem in solid state physics is that of an electron moving through a crystal. We would not be properly doing our job if we left you with the impression that quantum mechanics is used only for idealizations like square wells and harmonic oscillators. On the other hand, the aim of these pages is to provide simple examples to play with -- not the necessarily complicated real-world applications. And in a real crystal there are nearly infinite complications (and hence a wealth of observations seeking an explanation). The first problem is that a crystal with 10²³ electrons moving in it is clearly a many body problem whereas most of these pages deal only with one or two electron problems. Thus we consider here a "spherical cow": a 2D (!) array of potential wells (like nuclei) and electrons that interact only with those wells and not with each other. It should surprise you that such a distortion of reality is of much interest. When can we neglect electron-electron interactions and still see reality in our calculations? But even to handle such a simple case we will be forced to take on a new approach to "solution" of the problem: we will seek our "solution" using computer calculation rather than algebra. As a result much of the general will be lost, but I hope that in presenting a wide array of particulars you'll see the nature of the general solution which cannot be written down as a compact formula. This will also present you with a taste of how most physics calculations are actually performed.

Comments MailTo: tkirkman@guess.me