a=F/m=-g: acceleration is the result of applying the force; it can be calculated by the force divided by the particle's mass
z(t)=z0+v0t+½at2: the height of the object (z) depends on the initial height (z0), the initial velocity (v0) and time (t)
v(t)=v0+at: the velocity changes uniformly in time from its initial value
U(z)=-Fz=mgz: the potential energy has the property that if you take minus the derivative of it w.r.t. position, you get the force. -Fz + constant works; we've set the constant equal to zero.
In the case of the ball falling near the surface of the Earth, the above described motion cannot continue indefinitely as the ball soon encounters the ground. In the case of a perfectly elastic collision with the ground, the ground provides a force to exactly reverse the ball's velocity. It bounces forever between the ground (z=0) and some maximum height (zmax) that depends on its energy.
x(t)=A sin(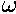 t+
t+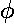 ):
the particle oscillates around equilibrium getting as far away as ±A. The period,
T (the time it takes to make one complete oscillation), is determined by
):
the particle oscillates around equilibrium getting as far away as ±A. The period,
T (the time it takes to make one complete oscillation), is determined by
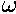 (the angular frequency): T=2
(the angular frequency): T=2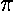 /
/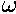 .
.
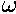 is in turn determined by the strength of the spring, k
(called the spring constant) and the mass m:
is in turn determined by the strength of the spring, k
(called the spring constant) and the mass m: 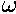 2=k/m.
Thus a strong spring connected to a light particle will oscillate quickly, i.e., with a short period.
2=k/m.
Thus a strong spring connected to a light particle will oscillate quickly, i.e., with a short period.
v(t)=A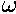 cos(
cos(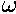 t+
t+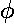 ):
the velocity (v) of the particle also oscillates, i.e., sometimes the particles is moving
to the right (positive v) sometimes it is moving to the left (negative v). Notice
that the particle has is maximum speed (of A
):
the velocity (v) of the particle also oscillates, i.e., sometimes the particles is moving
to the right (positive v) sometimes it is moving to the left (negative v). Notice
that the particle has is maximum speed (of A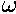 ) when the cosine term
reaches its extremes of ±1. That happens only when sine is zero (because
cos2
) when the cosine term
reaches its extremes of ±1. That happens only when sine is zero (because
cos2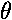 +sin2
+sin2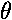 =1) and hence the particle is moving through the
equilibrium position (x=0). Similarly, the particle is momentarily at rest (v=0)
only when the particle is at an extreme position (±A; i.e., if cosine is zero,
sine must be ±1).
=1) and hence the particle is moving through the
equilibrium position (x=0). Similarly, the particle is momentarily at rest (v=0)
only when the particle is at an extreme position (±A; i.e., if cosine is zero,
sine must be ±1).
U(x)=½kx2: the potential energy has the property that if you take minus the derivative of it w.r.t. position, you get the force. ½kx2 + constant works; we've set the constant equal to zero.
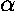 /r2 central force applied.
In intro physics the topic was the motion of planets under the influence of the Sun's gravitational
force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the
electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same"
as far a physics goes) but quite different distance scales. In addition energy emission by
gravitational radiation is totally negligible in the Solar System, whereas energy emission by
electromagnetic radiation (light) should be important in an atom.
/r2 central force applied.
In intro physics the topic was the motion of planets under the influence of the Sun's gravitational
force...orbital mechanics. In quantum mechanics the topic is the motion of an electron under the influence of the
electrostatic attractive force of the nucleus...atomic physics. Equivalent equations for the force (and hence "the same"
as far a physics goes) but quite different distance scales. In addition energy emission by
gravitational radiation is totally negligible in the Solar System, whereas energy emission by
electromagnetic radiation (light) should be important in an atom.
Planets move in ellipses with the Sun at one focus. Ellipses can be described in terms of their semi-major axis, a, (basically the longest radius) and their eccentricity (basically how squashed the ellipse is: e=0 is a circle, a fully squashed ellipse looks like a line and has e=1).
r=a(1-e2)/(1+e cos(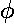 ));
rmin= a(1-e); rmax=a(1+e)
));
rmin= a(1-e); rmax=a(1+e)
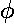 , the polar angle from closest approach is given the odd name:
true anomaly. The timing of the motion (i.e., when the planet or electron has
a particular
, the polar angle from closest approach is given the odd name:
true anomaly. The timing of the motion (i.e., when the planet or electron has
a particular 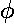 ) is a bit complex. The game is to express the
true anomaly (
) is a bit complex. The game is to express the
true anomaly (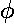 ) in terms of the eccentric anomaly (u)
and then find an expression relating time and the eccentric anomaly. For nearly
circular orbits it turns out that the true anomaly, the eccentric anomaly, and the
mean anomaly (
) in terms of the eccentric anomaly (u)
and then find an expression relating time and the eccentric anomaly. For nearly
circular orbits it turns out that the true anomaly, the eccentric anomaly, and the
mean anomaly (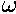 t) are all approximately
equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these
names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly,
the formula relating these two, and the formula relating time and the
eccentric anomaly.
t) are all approximately
equal to each other. I apologize for this archaic nomenclature, but physics is stuck with these
names. Below find the geometric construction that relates the true anomaly and the eccentric anomaly,
the formula relating these two, and the formula relating time and the
eccentric anomaly.
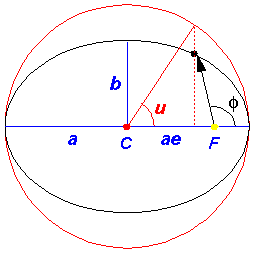
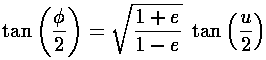
In the above picture, the yellow dot represents the Sun (or a nucleus); it is at a focus (F) of the ellipse. The red parts of the diagram have to do with the geometric construction for the eccentric anomaly which is measured from the center (C) of the ellipse. There is nothing physically at the center of the ellipse, this is all just part of a geometric construction. The blue parts of the diagram relate the semi-major axis (a) and the distance between the ellipse center and the focus (ae). The semi-minor axis, b, can be related to the semi-major axis and the eccentricity:
b = a(1-e2)½
The black ellipse is the orbit of the particle, i.e., the set
of positions the particle will traverse during a period
(T=2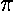 /
/ ).
).
The velocity vector is, of course, changing as the position vector is changing. The set of velocities the particle will have during a period is called the hodograph; it's just like an orbit, but for velocity rather than position. The hodograph is surprising: it's just a circle, but the center of the circle is not v=0.
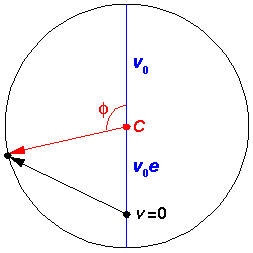
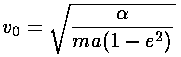
Note that at closest approach to the "Sun" (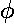 =0) the speed is a maximum
and the velocity points in the y direction, whereas at the far point
(
=0) the speed is a maximum
and the velocity points in the y direction, whereas at the far point
(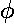 =180°) the speed is a minimum
and the velocity points in the -y direction. As the eccentricity
approaches 1, the maximum speed gets arbitrarily large and the minimum speed
approaches zero.
=180°) the speed is a minimum
and the velocity points in the -y direction. As the eccentricity
approaches 1, the maximum speed gets arbitrarily large and the minimum speed
approaches zero.
The above figures have been drawn with a rather large eccentricity: e=.707. For eccentricities similar to those of the planets it would be hard to distinguish the elliptical orbit from a circle (although for some planets--like Mars--the position of the Sun would look noticeably "off-center"...because the Sun is at a focus rather than the center).
If the (attractive) radial force is given by:
Fr=-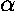 /r2, the
potential energy is U(r)=-
/r2, the
potential energy is U(r)=-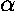 /r,
so that the minus derivative of U is
the force. Notice that just like the spring (which also attracts to the origin), the potential
energy is ever smaller as you approach the origin. Unlike the spring, this potential energy is
numerically negative (i.e., U(r)<0).
That is a result of our choice of additive constant. For the spring we choose the potential
to be zero at the origin, forcing the potential to be arbitrarily big as x approaches infinity.
For this problem we take the potential energy to be zero as r approaches infinity, so the potential
at the origin must be infinitely less, i.e., negative infinity.
/r,
so that the minus derivative of U is
the force. Notice that just like the spring (which also attracts to the origin), the potential
energy is ever smaller as you approach the origin. Unlike the spring, this potential energy is
numerically negative (i.e., U(r)<0).
That is a result of our choice of additive constant. For the spring we choose the potential
to be zero at the origin, forcing the potential to be arbitrarily big as x approaches infinity.
For this problem we take the potential energy to be zero as r approaches infinity, so the potential
at the origin must be infinitely less, i.e., negative infinity.
Most introductory courses in quantum mechanics start out with problems that are not one of the above classical problems: "square well" potentials also known as particle-in-a-box problems, and delta function potentials.