- On page 3 the recursion relation for the polynomial coefficients of a Hermite polynomial are given along with an example H10 polynomial. Show that the coefficients satisfy the recursion relation. Show that H10 satisfies the differential equation we found for H.
- Using the differential relationship on page 8 find H9 using H'10. Using "three term recursion relation" also on page 8, calculate H11 from H9 and x H10
- On page 8 there are two "why?"s. Provide explanations.
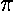 and hence
and hence 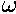 looks like it's 2
(see page 6).
looks like it's 2
(see page 6).
<k|x'|n> <k|x'2|n>
<k|p'|n> <k|p'2|n>
<k|x'p'|n> <k|p'x'|n>
Show p'x'-x'p'=-i
Use the above results to find 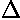 x' ×
x' × 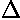 p'
in the nth eigenstate.
p'
in the nth eigenstate.
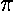
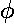 , i.e.,
, i.e.,
Prove this statement is true.We need not display similar plots for other times because the equation for
shows that plot for any other time is identical to the above except rotated by 2t' radians. Thus the lump will make one complete revolution in a period of
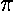
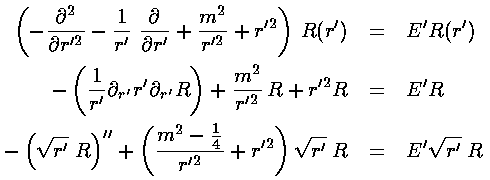
[Oddly enough the easiest starting point to change variables to s=ln(r') is the second equation, even though the third seems closest to WKB form.] Follow all the way through to find the WKB energies.
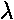 (r4-r2)
on the 3-d oscillator. When
(r4-r2)
on the 3-d oscillator. When 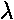 =1 we'd have our solution
to the r4 potential (but low-order perturbation theory is probably
not valid for such large
=1 we'd have our solution
to the r4 potential (but low-order perturbation theory is probably
not valid for such large 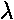 ). In any case the aim is to see how
the low-energy states (say E'<=7) move as a function of
). In any case the aim is to see how
the low-energy states (say E'<=7) move as a function of 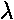 .
Note that since the perturbation is spherically symmetric, V' will not connect
different lm states. Find the energy shifts correct to second order for the
E'=7 degenerate set, and first order for E'<7.
The actual order of filling in nuclei seems to be: 1s, 1p, 1d,
2s. What value of
.
Note that since the perturbation is spherically symmetric, V' will not connect
different lm states. Find the energy shifts correct to second order for the
E'=7 degenerate set, and first order for E'<7.
The actual order of filling in nuclei seems to be: 1s, 1p, 1d,
2s. What value of 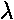 is consistent with the data?
is consistent with the data?
Note that for 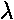 <0 (even slightly so) the bound states
are not stable, and will "leak". Explain. What is the meaning of the perturbation
theory in this case?
<0 (even slightly so) the bound states
are not stable, and will "leak". Explain. What is the meaning of the perturbation
theory in this case?
V'=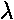 (r-1/r-r2)
(r-1/r-r2)
Find the first-order shifts for the 1s, 2s, and 3s levels.
Calculate the ratio of the (3s-2s) energy difference over
the (2s-1s) energy difference as a function of 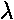 .
For the bottomonium system the ratio is (10.3553-10.0233)/(10.0233-9.460)=.59.
Find the value of
.
For the bottomonium system the ratio is (10.3553-10.0233)/(10.0233-9.460)=.59.
Find the value of 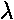 that works. For a pure oscillator this
ratio is 1, what is it for the pure -1/r potential (another possible
start for perturbation theory)?
that works. For a pure oscillator this
ratio is 1, what is it for the pure -1/r potential (another possible
start for perturbation theory)?
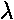 (x'2-y'2)
in the case of the 2-d oscillator. There are 4 degenerate E'=8 states, which we may consider either
in the |nxny> basis or in the |nrm> basis.
Follow this problem through as we did on page 15 where we did the 3-d case.
(x'2-y'2)
in the case of the 2-d oscillator. There are 4 degenerate E'=8 states, which we may consider either
in the |nxny> basis or in the |nrm> basis.
Follow this problem through as we did on page 15 where we did the 3-d case.