Index for 5½ Examples in Quantum Mechanics

1. Falling: Motion in a Linear Potential

   1. One Dimensional
      1. classical motion: PE, turning points, z(t), etc.
      2. length and energy scales
      3. Schrödinger's equation solution: Airy function
      4. graphs of solutions
      5. connecting classical variables and the wavefunction: WKB approximation
      6. QM "motion", Heisenberg uncertainty relation
      7. mathematical details of the above: superposition, time dependence
      8. approximation methods: WKB, Rayleigh-Ritz (variational), perturbation theory

   2. Two Dimensional
      9. classical ballistic (projectile) motion
      10. separation of variables
      11. QM force-free motion: a moving lump of probability density
      12. visualizing the moving lump of probability density
      13. falling motion (again)
      14. fire the quantum cannon

   3. Problems

2. Simple Harmonic Oscillator

   1. One Dimensional
      1. classical motion: PE, turning points, x(t), etc.
      2. length and energy scales
      3. Schrödinger's equation solution: Hermite polynomials
      4. graphs of solutions
      5. connecting classical variables and the wavefunction: WKB approximation
      6. QM "motion", Heisenberg uncertainty relation
      7. mathematical details of the above: superposition, time dependence
      8. raising and lowering operators

   2. Two Dimensional
      9. Schrödinger's equation solutions: xy 1D products, r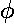: Laguerre polynomials
      10. degeneracy
      11. QM "motion": an orbiting wavefunction

   3. Three Dimensional
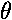
      12. Schrödinger's equation solutions: xyz 1D products, r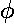: Laguerre polynomials
      13. visualizing the wavefunctions in 3D
      14. WKB approximation in 3D
      15. second order perturbation theory & degeneracy

   4. Problems

3. Hydrogen Atom
   1. classical motion: PE, turning points, Kepler's Laws, r(t), etc.
   2. length and energy scales
   3. Schrödinger's equation solutions: Laguerre polynomials
   4. radial plots of wavefunctions
   5. visualizing the wavefunctions in 3D
   6. two electron atoms
   7. exchange symmetry and spin-statistics
   8. spin-statistics theorem
   9. Aufbau: building up multi-electron atoms
   10. Stark effect
   11. crystal field theory
   12. chemical bonding

   13. problems

4. Square Wells

   1. One Dimensional
      1. classical motion: PE, turning points, x(t), etc.
      2. length and energy scales
      3. Schrödinger's equation solution: infinite square well
      4. finite square well: bound state solutions
      5. scattering from finite square well: reflection, transmission
      6. square barrier: tunneling

   2. Two Dimensional
      7. infinite rectangular square-well: xy separation
      8. round square-well: Bessel functions
      9. round finite square-wells: bound states
      10. reflection and refraction
      11. scattering from round infinite barrier: phase shifts, cross-section
      12. scattering from round finite square-well: rainbows, resonance

   3. Three Dimensional
      13. infinite 3D rectangular square-well: xyz separation
      14. spherical square-well: spherical Bessel functions
      15. visualizing the wavefunctions in 3D
      16. spherical finite square-wells: bound states
      17. scattering from spherical infinite barrier: solid angle, phase shifts, cross-section
      18. scattering from spherical finite square-well: glory, resonance

   4. Problems

5. Delta Function Potentials
   1. delta function basics
   2. dimensionless units for delta function potential
   3. isolated "atom"
   4. diatomic "molecule": bound states
   5. finite crystal: bound states
   6. theory for one cell after another
   7. bands in 1D crystal
   8. quantum motion in finite crystal
   9. scattering from a finite crystal

   10. Problems

6. Electrons in a Lattice: Band Structure
   1. lattice & lattice vectors; classical motion: PE, turning points, etc.
   2. Block wavefunctions; Schrödinger's equation; length and energy scales
   3. reciprocal lattice space
   4. grids: approximation to Schrödinger's equation in real space
   5. band structure in an empty lattice (i.e., free particle)
   6. numerical and exact solution to grided empty lattice
   7. numerical band structure for various potentials
   8. wavefunctions for various potentials
   9. Plane wave expansion aproximation
   10. discussion: relationship to classical considerations

   11. Problems